FÓRMULAS DEL MOVIMIENTO ONDULATORIO

Página diseñada en colaboración con Adriana Las

Pulsación: w = 2pf (rad/seg)

Periodo: T =  (seg)

Frecuencia: f =  (Hz)

Velocidad de las ondas transversales en una cuerda: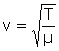

K =  (m^-1)

m: masa por unidad de longitud

velocidad de propagación: v = l f (m/s)

Ecuación del movimiento ondulatorio armónico o función de onda:

y (t, x) = A sen

Expresión de la función de onda: A sen (wt – kx)

Ecuación de la aceleración: a (t) = - Aw² cos (wt + j₀) ó a = -w²· x (t)

Fase del movimiento: wt + j₀

Energía mecánica total en la posición de equilibrio: E_M = Ec_máx =  m v²_máx

E = 2p² m A² f²

Energía mecánica total: E =  m w² A²

Energía cinética: E_C =  m v²

Energía potencial elástica: E_P =  K y²

Potencia de onda:  ( W )

Intensidad de una onda: I =  (J/s) ó (W/m²)

Intensidad de una onda esférica: I =  (W/m²)

Desde el mismo foco:

Velocidad en los sólidos:

E = módulo de Young o elasticidad de volumen (N/m² ó Pa)

d = densidad del sólido

Velocidad en los líquidos:

Q = módulo de compresibilidad del líquido (N/m² ó Pa)

d = densidad del líquido

Velocidad en los gases:

g = coeficiente adiabático (g_(aire) = 1’4)

P = presión del gas (Pa)

R = constante universal de los gases (8’314 )

M = masa molar del gas

d = densidad del gas

Nivel de intensidad sonora: b = 10 log (dB)

b = nivel de intensidad sonora (dB)

I = intensidad del sonido (W/m²)

I₀ = intensidad de referencia, umbral de audición, 1’0 · 10^-12 (W/m²)

En la ecuación de la elongación:

- Si el signo de kx = al signo de wt la dirección es de derecha a izquierda

- Si el signo de kx ¹ al signo de wt la dirección es de izquierda a derecha