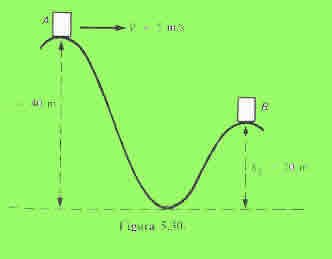En la cima de una montaña rusa el coche con sus ocupantes (masa total 1000 kg) está a una altura del suelo igual a 40 m y lleva una velocidad de 5 m/s. Calcula la energía cinética del coche cuando esté en la segunda cima que tiene una altura de 20 m. Se supone que no hay rozamiento.
Solución: 108.500 J
Una bala de 12 gramos lleva una velocidad horizontal de 250 m/s y se dispara contra un bloque de madera de 2 kg suspendido de una cuerda. La bala atraviesa el bloque y éste se eleva 5 cm. Hallar la velocidad con que sale la bala del bloque.
Solución: 91 m/s
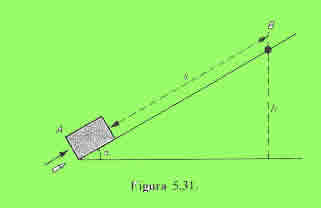Sobre un bloque de madera de 2 kg que se encuentra al comienzo de un plano inclinado 30º se dispara un proyectil de 100 g con una velocidad de 100 m/s incrustandose en él, como indica la figura. Si el coeficiente de rozamiento entre el bloque y el plano es 0,1, calcular la distancia que recorre el bloque sobre el plano.
Solución: 1,97 m.
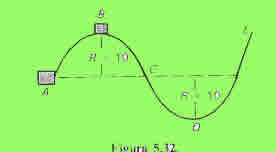Se quiere subir un cuerpo de 4 kg desde el punto A hasta el punto B a lo largo de un cuadrante esférico de 10 m de radio. Una vez en el punto B se le deja caer libremente a lo largo de la rampa BCD como indica la figura. No existe rozamiento. Calcular:
Solución: a) 392 J ; b) 19,97 m/s ; c) 10 m
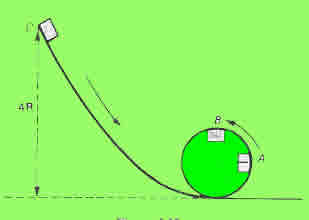Un cuerpo se desliza sin rozamiento por una vía en forma de rizo como indica la figura. Hallar:
Solución: a) 7,66·(R)1/2 ; b)6,2·(R)1/2 ; c) 2,5· (R)1/2
Un bloque de 5 kg choca con una velocidad de 10 m/s contra un muelle de constante elástica k = 25 N/m. El coeficiente de rozamiento entre el bloque y la superficie horizontal vale 0,2. Calcular la longitud que se comprime el muelle. La masa del muelle se considera despreciable.
Solución: 4 metros
1. Un hombre arrastra un cajón de 80 kg de masa una distancia de 15 m a lo largo de una superficie horizontal con velocidad constante. Calcular el trabajo realizado en los siguientes casos:
Solución: (a) 0; (b) 0; (c) 4704 J; (d) 4045 J.
2. Se lanza verticalmente hacia arriba un cuerpo de 225 g de masa con una velocidad de 100 m/s y vuelve al punto de partida con una velocidad de 95 m/s. Calcular la fuerza media de rozamiento del aire si alcanzó una altura de 495 m.
Solución: 0,11 N.
3. Una bomba accionada por un motor eléctrico ha elevado 100 m3 de agua a una altura de 20 m en 20 minutos. Si el motor tiene una potencia de 25 CV, calcular:
Solución: (a) 196·10-5; (b) 88 %.
4. Sobre un cuerpo de 15 kg, situado en una superficie horizontal, actúa horizontalmente una fuerza de 40 N. El cuerpo se ha desplazado 21 m en un minuto con aceleración constante. Calcular:
Solución: (a) 0.27; (b) 3,15 J; (c) 14 W.
5. Desde una altura de 50 m se deja caer un cuerpo de 500 g, si al llegar al suelo penetra en éste una distancia de 8 cm, calcular la resistencia media que ha ofrecido el suelo. Se desprecia el rozamiento con el aire.
Solución: 3062,5 N.
6. El punto de aplicación de la fuerza F = 3i - 2j + 5k N, se ha desplazado Dr = i + 4j — k. Hallar el trabajo realizado por la fuerza.
Solución: —10 J.
7. Un cuerpo de 100 g se deja caer desde un altura de 50 m en el mismo instante en que se lanza otro, de la misma masa, desde el suelo hacia arriba y en la misma vertical con una velocidad inicial de 20 m/s. Calcular
Solución: (a) 2,5 s; (b) 19,37 m; (e) 24,5 m/s, 4,5 m/s, ambos bajando; (4) 4,5 m/s, 24,5 m/s.
8. Se dispara un proyectil de 5 kg con una velocidad de400 m/s y un ángulo de elevación de 600. Si se desprecia la resistencia del aire, calcular la energía mecánica del proyectil en los siguientes casos:
Solución: 400.000 J en todos los casos.
9. La fuerza necesaria para alargar un muelle viene dada por F = 50 x N. Calcular la energía que adquiere el muelle cuando te le alarga 10 cm.
Solución: 0.25 J.
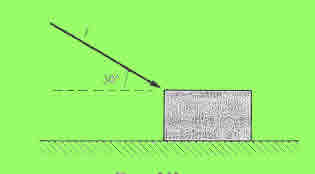10. Un bloque de 50 kg es empujado por una fueres que forma un ángulo de 300, tal como indica la Figura 5.35. El cuerpo se mueve con aceleración constante de0.5 m/s2. Si el coeficiente de rozamiento entre el bloque y el suelo es 0,2, calcular
Solución: (a) 161,8 N; (b) 2783.6 J; (e) 500 J.
11. Un cuerpo de 5 kg se desliza por una superficie horizontal sin rozamiento con una velocidad de 2 m/s. Si este cuerpo choca con un muelle cuya constante elástica vale 8 N/m.
Solución: (a) 1,58 m; (b) 0,2 m.
12. Hallar el trabajo realizado por la fuerza F = 2xi + 2yj desde el origen de coordenadas al punto P (1, 1) cuando la trayectoria que ha seguido el punto de aplicación ha sido la recta y = x.
Solución: 2 J.
13. Desde una cierta altura se deja caer un cuerpo de 1 kg sobre un muelle de altura despreciable que se comprime 15 cm. Si la constante recuperadora del muelle vale 500 N/m, calcular la altura desde donde ha caldo el cuerpo.
Solución: 0.57 m.
14. Desde una altura de 2 m se deja caer una pelota y después de rebotar en el suelo asciende hasta una altura de 1.9 m. Calcular
Solución: (a) 5 %; (b) 0.97; (e) 1.5 m.
15. Dos masas de 4 y 6 kg se mueven con velocidades respectivas de 5 y 3 m/s en la misma dirección pero en sentido contrario. Si el choque es inelástico, qué porcentaje de energía cinética se ha perdido en el choque.
Solución: 99.7 %
16. Un automóvil de 1425 kg parte del reposo sobre una pista horizontal. Suponiendo que la fuerza de rozamiento es constante y vale 15 kp, calcular
Solución: (a) 0,69 m/s2; (b) 904.200 J; (e) 51,2 CV; (d) 5374,7 m.
17. Un cañón de 30 cm de diámetro y 15 m de longitud, lanza un proyectil de 35 kg, con una velocidad inicial de 900 m/s, la cual va perdiendo por rozamiento con el aire, llegando al blanco con una velocidad de 540 m/s. Si el movimiento del proyectil en el interior del tubo es uniformemente acelerado, calcular:
Solución: (a) 27.000 m/s2; (b) 0,03 s; (e) 945.000 N; (d) 13,3·106 Pa (e) 1,4·107 J, 0,5·107 J.
18. Una bala de 20 g de masa se lanza horizontalmente sobre un bloque de madera de 2 kg suspendido por su centro de gravedad de un hilo inextensible, quedando empotrada en él. Después del impacto, el bloque oscila, experimentando un desplazamiento vertical de 10 cm. Calcular la velocidad que lleva la bala en el momento del impacto.
Solución: 141,4 m/s.
19. Dos masas iguales de 2 kg se mueven en la misma dirección y sentido con velocidades de 4 y 6 m/s. La más rápida alcanza a la más lenta produciéndose un choque elástico. Calcular la velocidad de cada una después de chocar.
Solución: 6 m/s, 4 m/s,
20. Dos esferas de 0,5 y 1 kg cuelgan del mismo punto mediante sendos hilos inextensibles de 1 es de longitud. Si la esfera más pequeña se la eleva hasta que el hilo forme un ángulo de 90º con la posición inicial y luego se la suelta para que caiga libremente. Calcular:
Solución: (a) 4,4 m/s; (b) —1,46 m/s, 2,9 m/s; (c) 0,1 m, 0,4 m.
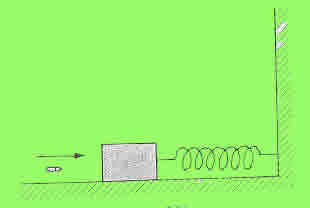21. Un bloque de madera está unido al extremo de un resorte como indica la Figura 5.36. Contra el bloque de 1 kg se dispara horizontalmente una bala de 200 g con una velocidad de 100 m/s quedando incrustada en el bloque. Si la constante elástica del muelle vale k = 200 N/m, calcular:
Solución: (a) 16,66 m/s; (b) 1,29 m.
22. Un muelle de constante recuperadora k 200 N/m está comprimido 10 cm. Una masa de 500 g está situada en el extremo del muelle. El muelle al descomprimirse empuja la masa y ésta sale despedida. ¿Cuál es la cantidad de movimiento con que la masa sale despedida?
Solución: 1 kg·m/s.
23. Se dispara un proyectil de 20 g contra un péndulo balístico de 8 kg. El péndulo se eleva 15 cm después que la bala se empotra en él. Calcular la velocidad de la bala.
Solución: 685,7 m/s.
24. Un vagón de 5 Tm que se mueve con una velocidad de 1 m/s choca con otro vagón de 10 Tm que está parado. Si en el momento del choque los dos vagones quedan enganchados, calcular la velocidad de los vagones después del choque.
Solución: 0,33 m/s
25. Desde una altura de 80 es se deja caer un cuerpo; 2 más tarde se lanza otro de idéntica masa desde el suelo hacia arriba y en la misma vertical. Si los dos cuerpos chocan en el punto medio del recorrido, calcular
Solución: (a) 51,2 m/s; (b) 1º. 42,9 m/s hacia arriba. 2º. 27,93 m/s hacia abajo.
26. Dos esferas elásticas de la misma masa se encuentran en la misma vertical separadas 90 m de distancia. La superior se deja caer libremente en el instante en que se lanza la otra hacia arriba de modo que choque en el preciso momento en que esta última invierte su sentido de movimiento. Calcular:
Solución: (a) 29,69 m/s; (b) 0 m/s, 29,7 m/s; (c) 9,8 m/s. 39,5 m/s, 41 m, 11,4 m.
27. Se quiere elevar 300 m3 de agua a una altura a 30 m en 1 hora. Para ello se instala un motor con un rendimiento del 70 %. ¿Qué potencia debe tener el motor?
Solución: 35.000 W.
28. Un bloque de 2 kg de masa está unido a un resorte comprimiéndole una longitud 20 cm. Si el bloque se deja libre recorre sobre una superficie horizontal una distancia de 2 m antes de pararte. Si la constante del muelle es 150 N/m, hallar el coeficiente de rozamiento entre la superficie horizontal y el bloque.
Solución: 0,07.
29. Dos esferas están suspendidas por das hilos paralelos de igual longitud. La masa de una de ellas es doble que la masa de la otra. Una de ellas se eleva 0,5 es soltándote posteriormente. A qué altura se elevará cada esfera después de chocar
Solución: (a) 0,05 m, 0,88 m; b) 0,22 m.
30. Se saca un clavo de 10 cm de longitud, totalmente introducido en una tabla, aplicando una fuerza constante cuya dirección es la del clavo. Dicho clavo fue introducido mediante 10 golpes de un martillo de 1 kg de masa, siendo su velocidad en el instante del golpe de 1 m/s. Despreciando las pérdidas energéticas así como la masa del clavo. Hallar la fuerza necesaria para desclavarlo.
Solución: 50 N.
31. Qué espesor debe tener un muro que opone una fuerza de rozamiento de 5000 N para que una bala de 50 g que incide formándo un ángulo de 60º con la horizontal, quede detenida a la mitad del muro. La velocidad de la bala es 400 m/s.
Solución: 1,6 m.
32. Se tiene un plano inclinado 60º respecto a la horizontal, cuya longitud es de 10 m ¿Qué velocidad paralela al plano debe comunicarse al cuerpo para que éste llegue a la parte superior del plano inclinado con velocidad nula?. El coeficiente de rozamiento vale 0,1.
Solución: 13,3 m/s.
33. Un cuerpo se mueve según la trayectoria x = t + 1; y = 2t— 2; z = t en m, y la fuerza que actúa sobre él es F = ti — (3t + l)j + 2k en N. Calcular el trabajo realizado por la fuerza en el intervalo de tiempo de t1= 2 s a t2 = 3 s.
Solución: —12,5 J.
34. En lo alto de un plano inclinado 30º de 2 m de longitud se coloca un cuerpo de 5 kg. El coeficiente de rozamiento del cuerpo con el plano inclinado y con el suelo es 0,1. Calcular
Solución: (a) 4 m/s; (b) 8 m.
35. Un avión de bombardeo que vuela a 600 km/h suelta una bomba de 50 kg cuando se encuentra a una altura de 800 tu. Calcular la energía mecánica de la bomba en los instantes siguientes:
Solución. 1.086.444 J en todos los casos.
36. Una masa de 2 kg que te mueve con una velocidad de 1 m/s, choca con otra masa de 4 kg que te mueve en la misma dirección, pero en sentido contrario con una velocidad de 4 m/s. Calcular la velocidad de cada masa después del choque:
Solución: (a) 2,3 m/s; (b) 0,66 m/s, 5,66 m/s; (e) 4,8 m/s, 1,08 m/s.
37. Se deja caer una pelota desde una altura de 2 m, y después de rebotar en el suelo sube hasta una altura de 1,5 m. Calcular
Solución: (a) 25 %; (b) 0.86.
38. Se quiere arrastrar por una superficie horizontal un cajón con velocidad constante de 15 km/h. Para ello te utiliza un motor de 10 CV. Si el coeficiente de rozamiento entre la superficie y el cajón es 0.25, calcular el peso del cajón:
Solución: (a) 721 kg (b) 540,8 kg.
39. Para introducir una estaca 20 cm en un terreno se han dado 10 golpes con un martillo de 2 kg. En cada golpe el martillo llega al extremo libre de la estaca con una velocidad vertical de 5 m/s. Calcular la resistencia que ofrece el terreno.
Solución: 1250 N
