Ejercicios Campo Electromagnético.

1e. Un protón se desplaza con una velocidad v = 2·10⁶ m/s y penetra dentro de un campo magnético uniforme, B = 3·10^-5 T, perpendicularmente. Calcular la fuerza electromagnética que experimenta y compararla con el peso del protón.

Datos: m_p = 1,67·10^-27 Kg; q = 1,6·10^-19 C; g= 9,8 N/Kg.

Solución: F = 9,6·10^-26 N.; Relación F/P = 5,8·10⁸

2e. En un campo magnético uniforme B = 12 T, que penetra perpendicularmente al plano del papel, entra un electrón con velocidad v_o = 4·10⁶ m/s perpendicular a B. Se pide a) un esquema del problema; b) la aceleración que adquiere el electrón; c) el radio de la trayectoria que describe; d) la frecuencia del movimiento.

Solución: b) 8,44·10¹⁸ m/s²; c) R = 2·10^-6 m; d) f = 336·10⁹ Hz.

3e. Un protón describe una circunferencia de radio 0,35 m dentro de un ciclotrón, antes de salir despedido. Calcular: a) la velocidad del protón en este instante; b) la frecuencia de la tensión alterna que se aplica en las D; c) la energía cinética que posee en MeV.

Datos: Campo magnético = 1,48 T.

Solución: a) v max = 5·107 m/s; b) f = 2,26·107 Hz; c) 12,86 MeV.

4e. En un campo magnético uniforme penetra un electrón con la velocidad v_o = 10⁷ m/s perpendicularmente al campo magnético y describe una trayectoria circular de 7,1 cm de radio. Calcular: a) el campo magnético existente; b) el periodo del ciclotrón.

Dato: e/m = 1,76·10¹¹ C/Kg

Solución: a) 8·10-4 T. b)  4,46·10-8 s.

5e. En el contorno de un triángulo rectángulo isósceles se dispone un hilo conductor de cobre recorrido por una corriente I. Se coloca dicho conductor en un campo magnético B normal al plano del conductor. Hacer el esquema de las fuerzas electromagnéticas que actúan sobre los lados.

6e. Se coloca una bobina de 1.000 espiras en un campo magnético uniforme de 0,5 T. Si el radio de las espiras es de 2,5 cm y las recorre una corriente de 1,5 A. Calcular: a) el momento magnético de la bobina; b) el momento del par cuando campo y vector superficie forman un ángulo de 30º, c) el valor máximo de dicho momento.

Solución: a) 2,95 A·m2; b) 0,74 N·m; c) 1,48 N·m

7e. Calcular el campo magnético creado en el centro de una espira circular de radio R, recorrida por una corriente de intensidad I.

8e. Un campo magnético uniforme B penetra por la cara sur de una espira de radio R, paralelo al eje de la espira. Si por la espira circula una corriente I₁, determinar: a) la dirección y sentido de la fuerza que se crea en la espira; b) el valor de la fuerza que actúa sobre una media espira.

Datos: B = 0,02 T; I₁ = 0,5 A; R = 0,04 m.

Solución: b) 0,8 mN.

9e. Por tres conductores rectilíneos, paralelos y equidistantes pasa una corriente de 5 A del mismo sentido. Se pide: a) la posición de los puntos en los que el campo magnético resultante es nulo; b) el campo magnético resultante en el punto medio de uno de los lados de la sección de los conductores. Distancia entre los conductores, d = 6 cm.

Solución: b) 1,9·10^-5 T

10e. Por el conductor de la figura pasa una corriente I. Calcular el campo magnético creado en el punto P por los arcos de circunferencia de radios R₁ y R₂ y los segmentos rectilíneos radiales AD y BC.

Datos; j = 90º; R₁ = 2 cm; R₂ = 4 cm; I = 5 A.

Solución: 19,6·10-6 T.

11e. Por un conductor largo pasa una corriente I = 10 A y forma una espira circular de radio R tangente al conductor. Calcular el radio de la espira si el campo magnético en el centro de la espira vale B = 4·10^-5 T.

Solución: 0,21 m.

12e. Conocidos los valores de la constante dieléctrica del vacío e_o y de la permeabilidad magnética del vacío, mo, deducir la velocidad de la luz , c, en el vacío.

Solución: 3·108 m/s

Campo magnético.

Datos de las partículas que intervienen en los problemas que siguen:

protón (p)                   m_p = 1,67·10^-27 kg;               q_p = 1,60·10^-19 C

electrón (e)                m_e = 9,1·10^-31 kg                  q_e = -1,60·10^-19 C

deutón (d)                  m_d = 2 ·m_p                             q_d = q_p

partícula (a)               m_a= 4·m_p                               q_a= 2·q_p

1.      Un campo magnético uniforme, B = 0,8 T, dirigido en el sentido positivo del eje z (vertical) actúa sobre un protón que se desplaza siguiendo el eje y en sentido positivo, con velocidad v_o = 5·l0⁶ m/s. Calcular la fuerza magnética que recibe la partícula.

Solución: F = 0,64 i (pN)

2.      Un electrón penetra perpendicularmente dentro de un campo magnético uniforme B, de 0,02 T con velocidad  vo = l05 m/s. Deducir la trayectoria que describe y el tiempo, período, que tarda en recorrerla.

Solución: Circular. T = 1,79 ns.

3.      Un protón se desplaza dentro de un campo magnético uniforme, B = 0,8 T orientado según el eje de las Y positivo. Deducir la fuerza (valor, dirección y sentido) que actúa sobre el protón cuando se desplaza con velocidad: a) vo = 2·106 k m/s; b)vo = 4·106 i m/s; c)  vo = 3,5·106 j m/s.

Solución: F = -0,256 i (pN); F = 0,512 k (pN); F = 0

4.      Resolver el problema anterior si la partícula es: 1) un electrón; 2) un neutrón.

Solución: F = 0,256 i (pN); F = -0,512 k (pN); F = 0

5.      Calcular el campo magnético en el interior de un solenoide de 2.000 espiras y radio 0,04 m, si el hilo es de cobre de resistividad r = 0,018 mW·m y radio 0,20 mm, y se conecta a una tensión de 130 V.

Solución: B = 5,65·10^-3 T

6.      En el interior de un solenoide hay un campo magnético uniforme B = 0,6 T. Calcular: a) la fuerza que ejerce el solenoide sobre un conductor de 30 cm paralelo al eje del solenoide por el que pasan 4 A de corriente; b) la fuerza cuando el conductor forma un ángulo de 30º con el eje del solenoide.

Solución: F₁ = 0 ; F₂ = 0,36 N

7.      Si se aceleran una partícula a y un protón mediante una diferencia de potencial DV y penetran perpendicularmente en un campo magnético uniforme B; determinar: a) la relación entre las energías cinéticas con que entran en el campo magnético; b) la relación entre los radios de sus respectivas trayectorias.

Solución: E₁/E₂ = 2; R_a/R_p =

8.      Un conductor de 0,2 m situado en un campo magnético de B = 0,5 T forma con el campo un ángulo j = 45º. Si pasa por el conductor una corriente de 3,0 A: a) calcular la fuerza que se crea en el conductor; b) representar la variación de la fuerza si el ángulo varía de 0 a 90º.

Solución: F = 0,21 k (N); F_max = 0,3 k

9.      Por un conductor de 0,50 m de longitud situado en el eje de las Y pasa una corriente de 1 A en el sentido positivo del eje. Si el conductor está dentro de un campo magnético ,B = 0,010 i + 0,030 k T, calcular la fuerza que actúa sobre el conductor.

Solución: F = 1,5·10^-2 i – 5·10^-3 k; F = 1,6·10^-2 N

10. Un electrón de 1 eV de energía gira en órbita circular plana y horizontal dentro de un campo magnético uniforme B = 1,0·10-4 T dirigido perpendicularmente de arriba hacia abajo. Se pide: a) el radio de la órbita del electrón; b) el sentido de giro del electrón.

Solución: R = 0,034 m; T = 3,57·10^-7 s

11. En una región donde hay un campo eléctrico E = 1.000 k V/m, (vertical ascendente) y un campo magnético B = 0,5 j T (horizontal hacia la derecha) penetra un protón perpendicularmente a ambos campos, y se observa que no se desvía. Determinar el vector velocidad vo del protón.

Solución: v_o = -2·10³ i (m/s)

12. Por un conductor de 0, 12 m de longitud orientado según el eje de las Y circula una corriente de 3 A dirigida hacías las Y positivas. Si se coloca el conductor dentro de un campo magnético uniforme de 0,04 T dirigido según el eje positivo de las Z, calcular: a) la fuerza que ejerce sobre el conductor; b) lo mismo, si el campo magnético toma la dirección y sentido positivo del eje de las X; e) la fuerza, cuando el campo es paralelo al plano XOY y forma con el eje X un ángulo de 30º.

Solución: F₁ = 1,44·10^-2 i (N) ; F₂ = -1,44·10^-2 k (N) ; F₃ = -1,26·10^-2 k (N) ;

13. Una bobina plana de 0,03 m de radio consta de 30 espiras y se sitúa dentro de un campo magnético B = 0,6 T. Calcular el momento magnético y el momento del par que actúa sobre la bobina recorrida por una intensidad de 4 A, si el campo magnético forma con la normal al plano de la bobina un ángulo 9 de 60º.

Solución: m = 0,25 A·m² ; M = 0,13 N·m

14. En una cámara de ionización se inyecta hidrógeno y se obtienen iones H2+ que, posteriormente, se les acelera mediante una diferencia de potencial DV y penetran en un campo magnético uniforme B perpendicular a la velocidad de los iones vo Se pide: a) el sentido del campo B si el detector de los iones está a la derecha de la cámara de ionización; b) si el detector está a 20 cm del punto de salida de los iones, calcular la diferencia de potencial que se debe aplicar a los iones, DV, para que lleguen al detector. Datos: B = 0,08 T; masa del ion H2+ ; m = 3,34·10-27 kg.

Solución: DV = 1.533 V.

15. Dos espiras conductoras de radios iguales, dispuestas en ángulo recto una respecto de otra con centro común 0, las recorren las intensidades I1 = 6 A, e I2 = 8 A. Calcular el módulo y la dirección del campo magnético en el punto 0. Radio de las espiras R = 4p cm.

Solución: B = 5·10^-5 T.

16. Un electrón se mueve por una órbita circular de 0,5 m de radio, perpendicular a un campo magnético uniforme de B = 2,5 T. Determinar: a) la velocidad angular del electrón; b) el período del movimiento; e) la energía que posee en MeV.

Solución: w = 0,44·10¹² rad/s; T = 14,3 ps; E_c = 1,38·10^-5 MeV.

17. Un protón se desplaza siguiendo una trayectoria circular en un campo magnético uniforme, con la energía de 1,5 MeV. Hallar la energía que posee: a) un deutón; b) una partícula a, si ambas partículas describen la misma trayectoria que el protón.

Solución: E_c(d) = 0,75 MeV; E_c(a) = 1,5 MeV

18. La misma corriente eléctrica circula por dos conductores A y D paralelos y rectilíneos, distanciados 0,12 m. Si dichos conductores se repelen con la fuerza de 6·10-8 N/m determinar: a) el sentido de la corriente en los conductores; b) el valor de la corriente; c) la fuerza que ejercen por unidad de longitud sobre otro conductor C equidistante de los anteriores y en el mismo plano si circula por él una corriente de 0,2 A en el mismo sentido que la del A.

Solución: I = 0,19 A; F = 2,5·10^-7 N

19. Un electrón acelerado por una diferencia de potencial DV = 200 V penetra en el centro de un condensador plano de longitud L = 2 cm y separación de armaduras d = 1 cm, con una diferencia de potencial de Vi = 5 V. Hallar el ángulo de desviación en la salida del condensador y la desviación respecto de la dirección inicial.

Solución: a = 2,5·10^-2 rad; Dy = 2,5·10^-3 k (N)

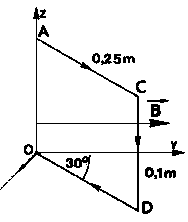
20. Una espira rectangular de 0,1 m ·0,25 m de lados está orientada como indica la figura dentro de un campo magnético uniforme B = 0,01 T en la dirección y sentido positivo del eje de de ordenadas. Calcular la fuerza que actúa en cada lado de la espira y el momento que experimenta si pasa por ella una corriente de 5 A.

Solución: M = -1,08·10^-3 k (N·m); F_AC = - F_DO = 6,25·10^-3 k (N)

21. Un electrón de 104 eV de energía se mueve horizontalmente y penetra en una región donde hay un campo eléctrico E = 100 V/cm dirigido verticalmente hacia abajo. A) Hallar la magnitud y dirección del campo magnético capaz de lograr que el electrón conserve su movimiento horizontal en presencia de ambos campos; b) si fuera un protón, ¿cómo debe ser B para conseguir el mismo resultado? La acción de la fuerza de la gravedad se puede despreciar.

Solución: B₁ = -1,69·10^-4 i (T); B₂ = 7,22·10^-3 i (T)

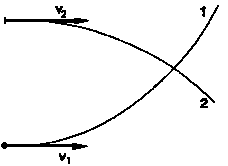
22. En una cámara de burbujas se observan las trayectorias de las partículas (1) y (2); la partícula (2) es un protón. A) Si el campo magnético B es perpendicular al plano de las trayectorias, deducir el sentido del campo B. B) El radio de curvatura de la trayectoria (2) es R2 = 14 cm y B = 1,5 T; deducir la cantidad de movimiento del protón. C) Si el radio de curvatura de la partícula (1) es R1 = 7 cm, deducir el signo de la carga de la partícula (que es carga elemental), y la cantidad de movimiento de la misma.

Solución: p₂ = 3,36·10^-18 kg·m/s; p₁ = -1,68·10^-18 kg·m/s

23. En el referencial (O; i, j, k) un hilo conductor de dirección Oj tiene una corriente de intensidad I = 10 A en el sentido positivo del eje de las Y. Si además un campo magnético B = 10-4 i T, calcular el campo magnético resultante en los puntos A(0,0,2), C(2,0,0), D(0,0,-1) en unidades del SI.

Solución: B_A = 1,01·10^-4 T; B_C = 1,000·10^-4 T; B_D = 0,98·10^-4 T

24. 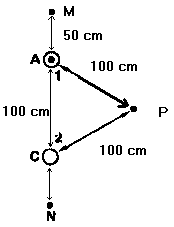Dos hilos rectilíneos, paralelos y horizontales están separados 100 cm; por el A pasa una corriente IA = 3 A dirigida hacia fuera del plano de la figura. Determinar: a) la intensidad y el sentido de la corriente en el conductor C si el campo magnético en el punto N es nulo; b) La intensidad del campo magnético en los puntos M y P creados por ambas corrientes.

Solución: B_M = -10,6·10^-7 j (T) ; B_P = 5,3·10^-7 T