Dinámica de los sistemas de partículas.

1. Dos masas de 6 y 9 Kg. se encuentran separadas 3 m, ¿dónde está situado el centro de masas?
2. Hallar el centro de masas de un alambre homogéneo que tiene forma de triángulo equilátero de 1 m de lado.
3. En un disco homogéneo de radio R se ha practicado un agujero circular de radio 1/2 R como muestra la figura. Hallar el centro de masas de la pieza.
4. Las posiciones y velocidades de tres partículas que avanzan en el eje X son, en un instante dado: Calcular, en dicho instante:

   Masa en Kg.	Velocidad ( m/s )
   2	5
   4	-10
   6	10

   a)     cantidad de movimiento total del sistema;
   b)     velocidad del centro de masas.
5. Una partícula de 5 Kg. se mueve a 3 m/s en el eje X. Al cabo de 15 segundos explota y se escinde en dos partes de 4 y 1 Kg.. La fracción de 4 Kg. se mueve formando un ángulo de 30º con dicho eje, a 9 m/s. Calcular la posición del centro de masas 10 s después de la explosión.
6. Un vaso, inicialmente en reposo sobre una mesa, estalla de forma espontánea en tres trozos que se mueven horizontalmente sobre la mesa. Dos de ellos, de igual masa, salen disparados con la misma velocidad de 10 m/s, formando entre sí un ángulo de 37º. El tercero tiene una masa triple de uno de los otros. Hallar la velocidad M tercer fragmento y la dirección en la que se mueve. ¿Qué velocidad posee el centro de masas inmediatamente después de la explosión?
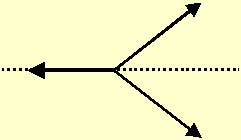
7. Una granada, moviéndose horizontalmente a 2 m/s, explota en tres fragmentos de masas: m/2, m/3 y m/6, respectivamente. Después de la explosión, el segundo fragmento se mueve horizontalmente a 5 m/s, el primero forma un ángulo de 45º con la horizontal y el tercero, un ángulo de –45º. Calcular las velocidades del primer y tercer fragmento.
8. En la figura se muestra el sistema formado por un muelle comprimido por dos cuerpos A y B de masas m₁ = 2 Kg. y m₂ = 5 Kg., que se encuentran en reposo sobre una superficie horizontal sin rozamiento. Al soltar estos cuerpos de forma simultánea, el cuerpo A sale despedido con v = 4 m/s. Calcular la velocidad del cuerpo B y la energía cinética del sistema, antes y después de soltar dichos cuerpos.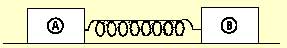
9. Dos cuerpos de masas m1 = 1 g y m2 = 5 g están en reposo separados entre sí 10 cm en una superficie horizontal. Están cargados eléctricamente de modo que se atraen. Si los soltamos, ¿a qué distancia de la posición inicial de m1 chocarán?
10. Sobre un vagón de mercancías descubierto que avanza libremente en una vía horizontal cae bruscamente un alud de nieve. La masa del vagón es de 20.000 Kg.; la masa de la nieve, de 4.000 Kg. y la velocidad inicial del vagón era de 54 km/h. ¿Cuál es la velocidad del vagón con la nieve?
11. Un patinador de 70 Kg. lanza un cuerpo de 1 Kg. a 20 m/s hacia adelante. Describir lo que ocurre, si el coeficiente de rozamiento entre los patines y el suelo es 0,1.
12. Un pez de 8 Kg. está nadando con v = 0,5 m/s hacia la derecha. Se traga otro pez de 0,25 Kg. que nada hacia él a 1,5 m/s. Calcular la velocidad del pez mayor inmediatamente después de tragarse al pequeño.
13. Un hombre de 60 Kg. va corriendo a 8 km/h y da alcance a una carretilla de 80 Kg. que marcha a 2,9 km/h, montándose en ella. Calcular la velocidad adquirida por la carretilla inmediatamente después de subirse el hombre.
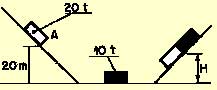
14. En el punto A de la figura se rompen los frenos de un vagón de 20 t en reposo. Debido a esta circunstancia, el vagón desciende por la rampa y en el tramo horizontal choca con otro vagón que se encuentra en reposo, al que no se le han aplicado los frenos, de masa 10 t. Ambos vagones quedan empotrados y se dirigen hacia la pendiente de la derecha, por la que suben hasta detenerse a una altura H. Calcular la altura H, despreciando el rozamiento en todos los tramos.
15. Un automóvil de 2.000 Kg. avanza a lo largo de una calle, en dirección Este, y choca a la velocidad de 50 km/h con un camión de 4 t que atraviesa la misma calle en dirección Sur, a la velocidad de 20 km/h. Como consecuencia del choque, ambos vehículos quedan unidos; ¿cuál es la magnitud y dirección de su velocidad inmediatamente después del choque?
16. Sea M la masa de un péndulo balístico de longitud L. Hallar la velocidad del proyectil de masa m si el péndulo sube hasta quedar el hilo horizontal.
17. Un proyectil de 10 g se dispara horizontalmente contra un bloque de madera de 4 Kg. en reposo sobre un suelo horizontal con un coeficiente de rozamiento 0,25. La bala queda incrustada en la madera y el conjunto recorre 1,84 m hasta pararse. Calcular la velocidad del proyectil en el momento de chocar con la madera.
18. Dos bloques de masas respectivas 15 y 5 g se mueven en la misma dirección, pero en sentido opuesto, con velocidades de 10 y 5 m/s, respectivamente. Calcular sus velocidades después del choque elástico.
19. Resolver el problema anterior suponiendo que ambos cuerpos avanzan en el mismo sentido y que el más lento es alcanzado por el más rápido.
20. Un péndulo simple de 2 m de longitud se separa de su posición de equilibrio un ángulo de 37º y se abandona libremente. Calcúlese:
    a) su velocidad en el punto más bajo de la trayectoria;
    b) si la masa del péndulo es de 100 g y choca con otra masa puntual de 200 g situada en ese punto, ¿cuál será la velocidad de cada una de las masas después del choque, si es completamente elástico?
21. Una bola de jockey B, en reposo sobre una superficie lisa de hielo, es golpeada por una segunda bola A, de igual masa, que se mueve inicialmente a 24 m/s y desviada 30º de su dirección inicial. La bola B adquiere una velocidad que forma un ángulo de 45º con la velocidad inicial de A. Calcular la velocidad de cada bola después del choque y discutir si es elástico.
22. Una bala de 10 g choca contra un bloque de 990 g que se encuentra en reposo sobre una superficie horizontal lisa, quedando incrustada en él. El bloque está unido a un resorte cuya constante elástica es 1 N/m. Si el choque comprime el resorte 10 cm, calcular:
    a)     velocidad del bloque inmediatamente después del choque;
    b) velocidad inicial de la bala.
23. Una partícula de 2 Kg. se mueve con velocidad de 4i m/s y su vector de posición, en el instante inicial, es 6j metros. Calcular su momento angular respecto del origen de coordenadas.
24. La ecuación del movimiento de un cuerpo de 2 Kg. es: r = 3t i- 2t² j. Calcular el momento angular del cuerpo respecto del origen de coordenadas en el instante t = 5 s.
25. Un objeto pequeño está unido a una cuerda que pasa por el interior de un tubo, como indica la figura. El objeto describe un movimiento circular de 0,5 m de radio en el plano horizontal, con velocidad angular de 20 rpm. Al tirar de la cuerda hacia abajo se reduce el radio de la trayectoria. ¿Cuál es la velocidad angular cuando el radio mide 0,25 m?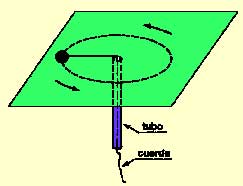

Soluciones a los problemas:

5.1.           A 1,8 m de la partícula de 6 Kg..

5.2.           Xcm = 0,5 m ;  Ycm = 0,29 m.

5.3.           Xcm = 0 ;   Ycm  = (1/6)R.

5.4.           a)30 i Kg·m/s  ;  b) 2,5 i m/s.

5.5.           75 m.

5.6.           6,3 m/s ; 198,5º ; 0 m/s.

5.7.           v1 = 5,2 m/s    v3 = 15,6 m/s.

5.8.           v_B = 1,6 m/s ;  Ec (antes)  = 0 J   Ec (después) = 22,4 J.

5.9.           8,3 cm.

5.10.       45 km/h ( 12,5 m/s).

5.11.       retrocede 4 cm.

5.12.       0,44 m/s.

5.13.       5 km/h (1,4 m/s).

5.14.       8,9 m.

5.15.  21,3 km/h (5,9 m/s)  ;  38º 39' Sudeste.

5.16.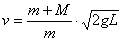 

5.17.       1.203 m/s,.

5.18.       v₁₅ = 2,5 m/s    v₅ = 17,5 m/s.

5.19.       v₁₅ = 7,5 m/s    v₅ = 12,5 m/s.

5.20.       a) 2,8 m/s;     b) v₁₀₀ = - 0,93 m/s;     V₂₀₀  = 1,87 m/s.

5.21.       V_A =  17,6 m/s ;  V_B = 12,4 m/s. No se conserva la energía cinética.

5.22.       a) 0,1 m/s; b) 10 m/s.

5.23.       – 48 k.

5.24.       – 300 k.

5.25.       w= 8,38 rad/s (= 80 rpm).