Fenómenos ópticos

P 00. ¿Qué tienen en común la reflexión y la refracción y en que se diferencian?

 

P 001. Dibuja la marcha de un rayo luminoso que pasa:

 

P 01.Cuando la luz pasa de un medio transparente a otro distinto, ¿varía su frecuencia?¿varía su velocidad?¿y su longitud de onda? Razona tus respuestas.

P 02. Una fuente luminosa puntual emite luz cuya longitud de onda en el vacío es de 600 nm. A 6 cm. de ella se encuentra situada una pantalla y entre ambos se dispone una lámina de vidrio de 6 mm de espesor e índice de refracción 1,5. ¿Cuántas ondas habrá entre la fuente luminosa y la pantalla?

P 03.¿Cuál es el índice de refracción del vidrio respecto al agua, si el índice de refracción del agua respecto al aire es 4/3 y el del vidrio respecto al aire es 3/2?

P 04.Un haz luminoso incide sobre una lámina de vidrio, de índice de refracción 1,50. ¿Cuál ha de ser el ángulo de incidencia,f, para que el de refracción sea f/2?

P 05.Un cubo de vidrio de índice de refracción 1,5 se encuentra situado en el aire. Un haz de rayos paralelos penetra oblicuamente a través de la cara superior del cubo y después incide sobre una de sus caras laterales. ¿Pueden los rayos salir a través de esta cara?

P 06.Un foco luminoso puntual se encuentra sumergido 40 cm. por debajo de la superficie del agua. Hallar el diámetro del círculo mayor en la superficie del agua, a través del cual la luz puede salir al exterior.

P 07.La sección de un prisma óptico tiene la forma de un triángulo rectángulo isósceles. ¿Cuál es el valor mínimo de su índice de refracción para que un rayo de luz se refleje totalmente en ángulo recto?

P 08.Un rayo luminoso incide sobre un prisma óptico con un ángulo de incidencia de 90º y tras refractarse en la segunda cara emerge del prisma con una ángulo de refracción de 9,25 º. Hallar el índice de refracción del prisma, sabiendo que su ángulo es f =50º.

P 081. Determinar el índice de refracción de un prisma de ángulo 40º, sabiendo que un rayo incide con un ángulo de incidencia de 40º sigue una trayectoria paralela a la base del prisma.

P 082. ¿Cuál es el ángulo límite para la luz que pasa del vidrio (n = 1,5) al agua (n = 1,33)?

P 09.¿Cuál es el ángulo de desviación mínima para un prisma de vidrio (n = 1,59) cuyo ángulo es de 60º?

P 10.El prisma de la figura tiene un índice de refracción de 1,5. Sobre su cara inferior incide un rayo luminoso procedente del aire y sigue a continuación la dirección indicada. Si f =30º y la base del prisma es plateada, hallar el ángulo f que forma el rayo saliente con la normal a la segunda cara del prisma.

Falta dibujo

 

P 11. ¿Qué diferencia existe entre la interferencia y difracción? Explícalo claramente, ayudándote de ejemplos, si lo juzgas conveniente.

P 12. Aunque podemos oír detrás de las esquinas, no podemos ver alrededor de ellas. ¿Cómo se puede explicar esto, si tanto la luz como el sonido son ondas?

P 13. ¿Por qué si se encienden dos linternas muy  próximas y se proyecta su luz sobre una pantalla no se producen fenómenos de interferencia ¿Por qué en el experimento de la doble rendija de Young se emplea luz monocromática?

P 14. Dos rendijas paralelas y estrechas, a 0,25 mm de distancia, se iluminan con luz verde de 436,1 nm de longitud de onda. Sobre una pantalla situada a 1,2 de distancia del plano de las rendijas se producen las correspondientes franjas de interferencia. Hallar la distancia del máximo central a la primera franja brillante situada a cada uno de sus lados.

P 15. En un experimento de Young con luz monocromática la distancia entre las rendijas es de 0,5 mm y en la pantalla, situada a 3,3 m de distancia, se observa el primer máximo brillante a 3,4 mm del centro. ¿Cuál es la longitud de onda de la luz?

P 16. Suponiendo que los faros de un coche sean puntuales, ¿cuál será, aproximadamente, la distancia máxima al coche a la que puede situarse un observador para que los dos faros se distingan uno de otro?

 P 17. Un disco compacto, al reflejar la luz, muestra una apariencia multicolor, que varía según la orientación del disco respecto al ojo y a la fuente luminosa. ¿A qué se puede deber este hecho?

 

Página de Actividades

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Respuesta a las cuestiones.

 

 

 

 

 

 

 

 

 

S 2. La longitud de onda de la luz en el vacío es : l0 = 600 nm, y en el vidrio l = l0/n = 600 nm/ 1,5 = 400 nm.

La luz recorre 6 cm – 0,6 cm = 5,4 cm en el aire y 0,6 cm en el vidrio.

En los 5,4 cm del aire existen:

Y en los 0,6 de vidrio:

Por lo tanto, entre la fuente y la pantalla habrá: 90.000 ondas + 15.000 ondas = 105.000 ondas.

 

 

 

 

 

 

 

 

 

 

 

S 3.

 

 

 

 

 

 

 

 

 

 

 

S 4. Aplicando la ley de Snell: n1·sen i = n2·sen r, y teniendo en cuanta que en este caso: n1 = índice de refracción del aire = 1; n2 = índice de refracción del vidrio = 1,50; i = r; r = q/2, resulta: sen q = 1,50·sen q/2.

Aplicando la fórmula que el valor del seno del ángulo doble, se tiene: 2senq/2·cosq/2=1,50senq/2, y simplificando: cosq/2=0,75, de donde se obtiene finalmente: q = 82º50´.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 5. Para que los rayos puedan salir a través de la cara lateral del cubo han de incidir sobre ella con un ángulo i2 menos que el límite. Él valor de este ángulo es :

Sen L = n2 / n1 = 1 / 1,5 = 0,6667 Û L 0 41,81º. Por lo tanto: i2 < 41,81º y, en consecuencia (ver la figura), el ángulo de refracción en la cara superior habrá de ser: r1 > 48,19º.

Aplicando la ley de Snell a la refracción de esta cara, tenemos:

n2·sen i1 = n1·senr1 Û sin i1 = (n1/n2)·sen r1> 1,5·sen 48,19º = 1,5·0,7453= 1,118.

Este valor de sen i1 resulta imposible. Por tanto, los rayos luminosos no pueden salir por la cara lateral.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 6. Los rayos luminosos procedentes del foco puntual y que se refractan saliendo del agua están contenidos dentro de un cono cuyo semiángulo en el vértice es: Sen L = n2 / n1 = 1 / (4/3)= 3/4 Û L = 48,59º.

El diámetro del círculo será el diámetro de la base del cono:

D = 2R = 2·40 cm·tan 48,59º = 91 cm

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 7. Para que la luz se refleje en ángulo recto (ver la figura) ha de incidir sobre la cara mayor del prisma con un ángulo i = 45º, y para que esto suceda se debe cumplir que el ángulo límite correspondiente a la superficie de separación aire-vidrio sea inferior o igual a 45º; es decir Sen L = n2 / n1 £ , siendo n1 el índice de refracción del vidrio y n2 el del aire (n2 = 1). Por tanto:  y el índice de refracción mínimo será igual a

 

 

 

 

 

 

 

 

 

 

 

 

S 8. Aplicando la ley de Snell a las refracciones que tienen lugar en las dos caras del prisma, y designando por n su índice de refracción, resulta: sen 90º = n·sen r1 Û 1 = n·sen r1; n·sen i2 = sen 9,25º; n·sen i2 = 0,1607.

Por otra parte r1 + i2 = f = 50º.

Resolviendo ahora el sistema formado por estas tres ecuaciones obtenemos n = 1,45

 

 

 

 

 

 

 

 

 

 

 

 

S 9. El índice de refracción del prisma está relacionado con el  ángulo del vértice f y con la desviación mínima dm por medio de la expresión: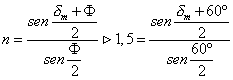  

de donde resulta que dm = 37,18º.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 10. El rayo entrante experimenta  sucesivamente los fenómenos de refracción, reflexión y refracción.

Primera refracción. Como el ángulo de incidencia es de 60º, aplicando la ley de Snell se tiene: 1·sen 60º = n·sin r1; de donde r1 = 35,26. El rayo refractado forma con la horizontal un ángulo de 30º + 35,26º = 65,26º.
Reflexión. El rayo procedente de esta primera refracción incide sobre la cara horizontal formando con la normal un ángulo de 90º - 65,26º = 24,74º. En esta cara el rayo se refleja con un ángulo de reflexión de 24,74º.
Segunda refracción. El ángulo de incidencia será: i2 = 30º - 24,74º = 5,26º. Aplicando la ley de Snell se cumple: n·sen 5,26º = sen j , de donde j = 7,9º.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 11. Los fenómenos de interferencia y difracción se encuentran totalmente relacionados. En efecto,  los fenómenos de difracción se observan como consecuencia de las interferencias que tienen lugar entre los rayos difractados. Las zonas oscuras de las figuras de difracción se deben a interferencias destructivas entre dichos rayos, y las claras, a interferencias contractivas.

 

 

 

 

 

 

 

 

 

 

 

 

S 12. El “oir detrás de las esquinas” es un fenómeno de difracción del sonido. El fenómeno análogo no se aprecia en el caso de la luz, pues para que se produzca difracción se requiere que el tamaño del obstáculo sea similar al de la longitud de onda de la luz visible, que es inferior al micrómetro.

 

 

 

 

 

 

 

 

 

 

 

 

S 13. Para que dos rayos luminosos produzcan interferencias permanentes es necesario que:

    • Ambos sean de la misma frecuencia: es decir, de la misma longitud de onda.
    • Su diferencia de fase permanezca constante.
    • Se hallen en el mismo estado de vibración (es decir, que si se trata de rayos de luz polarizada, vibren en el mismo plano;  y si es luz natural, su estado de vibración, en los diferentes planos posibles, sea el mismo en ambos rayos).

Estas condiciones reciben el nombre global de condiciones de coherencia.

La única forma posible de conseguir esta coherencia es que los dos rayos de luz procedan del mismo foco. Hay que tener en cuenta que, como la luz se debe a vibraciones que se producen en los átomos excitados del foco emisor cuando sus configuraciones electrónicas se modifican, resulta imposible que dos focos luminosos diferentes den lugar a fenómenos de interferencia, puesto que nunca coincidirán las fases de vibración de todos los átomos de un foco con los del otro. Por consiguiente, la diferencia de fase de los dos rayos que incidan en un punto estará variando continuamente, y el ojo humano sólo podrá percibir el valor medio de la intensidad luminosa, que será también fluctuante.

Esto explica que dos linternas (focos diferentes) no puedan producir interferencia, y que en el experimento de la doble rendija de Young se utilice luz monocromática (una sola frecuencia)

 

 

 

 

 

 

 

 

 

 

 

 

 

S 14. La posición de las franjas brillantes viene dada por:

Para la primera de estas franjas, m = 1. Por lo  tanto:

 

 

 

 

 

 

 

 

 

 

 

 

 

S 15. Es la primera franja brillante, por tanto:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S 16. Se trata de un fenómeno de difracción de Fraunhofer producida por la una abertura (la de la pupila del ojo). La distancia máxima del observador, D, para que los dos faros del coche se distingan separadamente viene dada por:

Siendo Dl la distancia entre los dos faros, que consideramos igual a 1,4 m; l, la longitud de onda de la luz emitida (suponemos un valor medio de 550 nm), y a, el diámetro de la pupila del ojo (5mm). Sustituyendo estos valores numéricos en la expresión anterior, tenemos que:

 

 

 

 

 

 

 

 

 

 

 

 

 

S 17. La superficie de los discos compactos tiene una pista acanalada, con surcos cuyo espaciado es de aproximadamente 1 mm, y que actúa como una rejilla de difracción. La luz dispersada por estos surcos da lugar a interferencias constructivas sólo en ciertas direcciones que dependen de la longitud de onda y de la dirección de la luz incidente. Cualquier sección del disco actúa como rejilla de difracción para la luz blanca, originando distintos colores según la dirección. Por eso, al variar la posición u orientación de la fuente luminosa, del disco o del observador, varían los ángulos de incidencia y de difracción y el disco ofrece una apariencia multicolor.