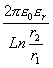Solución: a) g = 4 go ; b) No ; c) 6 horas.
Solución:
![]()
a) ¿qué velocidad deben comunicar los cohetes para que tenga lugar ese movimiento?
b) ¿cuánto vale el trabajo realizado para llevarlo de la superficie de la Tierra a esa altura?
c) ¿cuál es la energía total del satélite?
Datos: RTierra = 6,36×106 m; g0 = 9,8 m/s-2
Solución: a) v = 7.809 m/s ; b) W = -1,61·109 J; c) ET = -3,659·1010 J
Datos: R = 6370 Km; G = 6,67×10-11 SI.
Solución: M = 1,88·1024 Kg
Solución:
a) g = 0; b) g = ![]() ; c) g =
; c) g = ![]()
Calcular expresiones para el potencial
gravitatorio terrestre en tres puntos cuyas distancias r al centro de la
Tierra sean, respectivamente: a) r > RT; b) r = RT;
c) r < RT. (Se supone la densidad constante).
Solución: a) V = ![]() ; b) V =
; b) V = ![]() ; c) V =
; c) V = ![]()
Considérense cuatro masas puntuales
iguales de valor m colocadas en los vértices de un cuadrado de lado 1. Calcular
el campo y el potencial: a) en un punto P situado sobre la perpendicular
al plano del cuadrado por su centro y a distancia 1; b) en el centro del
cuadrado. Calcular además la velocidad de una masa m abandonada en reposo
en el punto P al llegar al centro del cuadrado.
Solución: gp = ![]() ; Vp =
; Vp = ![]() ; b) go = 0 ; Vo =
; b) go = 0 ; Vo =
![]() ; vo =
; vo = ![]()
Solución: v1 = 1,11944·104 m/s ; v2 = 1,11933·104 m/s ; v1-v2 = 1,1 m/s
Solución: Vp = 20.400 V; Ec = 4.382,5 N/C ; j = -58,28º
Solución: Vc = 6·104 V ; Ec = 1,73·104 N/C
a) el valor del potencial electrostático en un punto A situado en el eje X a 4 m del origen.
b) el campo electrostático en dicho punto;
c) el trabajo realizado para llevar una carga puntual de 1 C desde el punto A a otro B de coordenadas (4, 3).
Solución:
a) VA = - 33,75 V; b) ·EA = 6,76 N/C ; j = 129,72º ;
c) ![]() = 9,45 J.
= 9,45 J.
Datos: masa de cada esfera 10 g; K = 9 × 109 N m2 C-2; g = 10 m/s ; cos 300 = 0,867.
Solución: q = 2,5 mC; T = 0,115 N.
Un campo eléctrico uniforme de valor E = 200 N/C está dispuesto
horizontalmente en la dirección del eje X. Se deja en libertad en el origen,
y partiendo del reposo, una carga puntual de Q = 3 uC y masa = 0,12 g. Calcular:
a) la energía cinética de la carga en x = 4 m;
b) la variación de la energía potencial en el mismo recorrido;
c) el desplazamiento vertical que ha experimentado la partícula;
d) la diferencia de potencial eléctrico entre la posición inicial y final
de la partícula.
Datos: g = 9,8 m/s2.
Solución: a) Ec = 1,08·10-2 J ; b) Ep = -1,08·10-2
J ; y = 7,78 m;
El potencial eléctrico en un punto del eje OX es: V(x)
= x2 - 3x. Calcular la intensidad del campo eléctrico y el potencial
en el punto x = 4 m.
Solución: E = -5 N/C; V = 4 v
Solución: x = 0,0176 mm.
Solución: ET =
Un electrón de carga 1,6 × 10-19
C está situado en un campo eléctrico uniforme de intensidad 120 kV/m. Determínese
la aceleración del electrón y el tiempo que tarda en recorrer 30 mm desde
el reposo. (me = 9,1 × 10-31 kg).
Solución: a = 2,1·1016
m/s ; t = 1,69 s
Dos placas metálicas horizontales y paralelas están separadas
2 cm. La diferencia de potencial entre ellas es de 120 V. Se pide :
a) la magnitud del campo eléctrico en el espacio comprendido entre las placas.
b) la fuerza que actúa sobre un electrón.
c) la energía que un electrón inicialmente equidistante entre las placas
gana al recorrer una distancia de 1 mm en una dirección que forma 30° con
las líneas del campo eléctrico.
Solución: a) E = 6·103
N/C; b) F = 9,6·10-16 N ; c) DE = 0
Una esfera conductora en equilibrio posee una carga superficial
de densidad d conocida, homogéneamente distribuida. Se sabe que a una distancia
L de su centro, el potencial es 1/10 del potencial de dicha esfera. Calcular
:
a) el radio de la esfera conductora;
b) la carga eléctrica de la esfera;
c) el potencial eléctrico de la esfera;
d) el campo eléctrico en un punto muy próximo a la superficie de la esfera.
¿Cuál será el valor del campo eléctrico en un punto del interior de la misma?
Solución: a) R = L/10 ; b) Q =
0,04 psL2 ; c) V = sL
/ 10ereo
Sean dos placas planas y paralelas conductoras, de superficie
S, grande en comparación con la distancia que las separa, uniformemente
cargadas con densidad +d y -d respectivamente. Supongamos que están separadas
por una distancia d, calcular :
a) el campo en un punto entre las placas;
b) la diferencia de potencial entre las placas;
c) Sabiendo que este par de placas forma lo que se conoce como un condensador
plano y que la capacidad de un condensador viene dada por la expresión C
= Q/V, calcular esta capacidad.
Solución: a) Et = ![]() ; b) V+ - V- =
; b) V+ - V- = ![]() ; c) C = ereo S/d
; c) C = ereo S/d
a) el campo en un punto del espacio entre las superficies cilíndricas;
b) la diferencia de potencial entre las superficies cilíndricas;
c) Sabiendo que dichas superficies constituyen un condensador cilíndrico y su capacidad viene dada por C=Q/V , calcula una expresión de la misma.
Solución: a)
E = ![]() ; b) V+ - V-
=
; b) V+ - V-
= 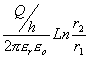 ; c)
; c)