Inducción electromagnética.

1e. En el campo magnético uniforme B = 0,04 T se coloca una bobina plana, de superficie S = 50 cm2, formada por 20 espiras, como indica la figura. Calcular el flujo magnético que la atraviesa.

Solución 2·10-3 Wb.

2e. En un campo magnético uniforme B = 0,2 T se coloca una bobina plana de N = 30 espiras de 12 cm2 de superficie, perpendicularmente a las líneas del campo; a) si se desplaza la bobina en un movimiento de traslación, ¿varía el flujo que la atraviesa?; b) si se le da un giro de 180º alrededor de un diámetro, ¿qué variación de flujo se produce?.

Solución: a) 0; b) –1,44·10-2 Wb.

3e. Una bobina rectangular plana de 100 espiras, de superficie 2·10-2 m2 cada espira, está dentro de un campo magnético uniforme, cuyas líneas de fuerza son perpendiculares a la cara de la bobina, Si el campo magnético varía en 0,1 s de 0,6 T a 0,3 T, calcular la f.e.m. inducida en la bobina.

Solución: 6 V.

4e. Una bobina plana de N = 400 espiras de radio r = 0,2 m, tiene inicialmente el eje paralelo a un campo magnético uniforme B, de intensidad B = 0,3 j T. Si en 0,5 s el eje de la bobina se coloca perpendicularmente al campo magnético, determinar: a) la f.e.m. inducida, b) la intensidad de la corriente; c) el sentido de dicha corriente. Dato: resistencia de la bobina, R = 11 W.

Solución: a) 30 V; b) 2,7 A.

5e. El circuito formado por los conductores paralelos, el galvanómetro y el conductor LL´ tiene una resistencia R. Si se desplaza LL´ con movimiento rectilíneo uniforme y velocidad ve dentro del campo magnético unirforme B, calcular: a) la fuerza de arrastre Fe, que se debe aplicar para que ve sea constante (se desprecian los rozamientos); b) la potencia aplicada y la potencia eléctrica producida.

5e. Una bobina plana, cuadrada, de 300 espiras y 5 cm de lado se sitúa perpendicularmente a un campo magnético uniforme de intensidad B = 0,8 T en un electroimán. Los extremos del hilo van unidos a un miliamperímetro de resistencia Ra = 2 W y la resistencia de la bobina es de R = 8 W. Calcular: a) la f.e.m. inducida si la corriente del electroimán disminuye y el campo magnético se anula en t = 12 s.; b) la intensidad de la corriente inducida y el sentido de la misma en la bobina.

Solución: a) 0,05 V; b) 5 mA

6e. Una varilla metálica de 1 m de longitud gira a la velocidad angular v = 20 rad/s, constante, en un campo magnético uniforme de intensidad B = 0,05 T. El eje de giro pasa por un extremo de la varilla y es paralelo a las líneas de fuerza del campo magnético. Calcular la f.e.m.. inducida entre los extremos de la varilla.

Solución: -0,50 V.

7e. Calcular el coeficiente de autoinducción L, de una bobina de N = 2.000 espiras de hilo uniforme de 60 cm de longitud y radio R = 4 cm.

Solución: 0,04 H.

8e. Una bobina de autoinducción L = 0,4 H se une a un generador de 12 V de f.e.m.. Calcular la variación de la intensidad de la corriente en el tiempo: a) al conectar la bobina a la batería; b) cuando la corriente alcanza el 50 por 100 del valor correspondiente a la ley de Ohm.

Solución: a) 300 A/s; b) 15 A/s.

9e. Calcular la energía magnética almacenada en una bobina de 500 espiras, de superficies S = 0,50 m2 y longitud l = 0,5 m, cuando transporta una corriente de 4 A.

Solución: 2,5 Julios.

10e. Se aplica una tensión de 220 V al circuito primario de un condensador que contiene 1.100 espiras y circula por él la intensidad de 45 mA. Si el secundario posee 50 espiras, calcular: a) la tensión del secundario; b) la intensidad del secundario; c) si el rendimiento del transformador es del 98 % indicar las causas de la pérdida de energía y la forma en que aparece esa energía perdida.

Solución: a) 10 V; b) 2 mA.

Las pérdidas de energía, aunque pequeñas, se deben al efecto Joule en las bobinas, a la calidad de las sustancias ferromagnéticas y a las corrientes de Foucault producidas en las chapas de hierro dulce del interior de las bobinas. La energía se disipa en forma de calor.

Inducción Electromagnética. Tema 11. Bruño Física COU.

  1. Una bobina plana de 40 espiras y superficie 0,04 m2 está dentro de un campo magnético uniforme de intensidad B = 0,10 T y perpendicular al eje de la bobina; si gira en 0,2 s hasta que el campo esté paralelo al eje de la bobina, calcular la f.e.m. inducida.

Solución: e = -0,8 V.

  1. Una bobina gira dentro de un campo magnético uniforme de B = 0,2 T a la velocidad de 20 rad/s. Calcular la f.e.m. inducida. Datos: Radio de la bobina, R = 6 cm; número de espiras N = 100.

Solución: e = 4,52 sen 20t V.

  1. Un solenoide de 500 espiras va enrollado alrededor de una barra de hierro dulce de 30 cm de longitud y la sección transversal es de 0,05 m2. Por el hilo circula una corriente I = 0,02 A; calcular: a) el campo magnético en el interior del solenoide; b) el flujo magnético que atraviesa la barra de hierro.

    Dato: permeabilidad magnética del hierro mr = 350.

Solución: B = 0,04 T; F = 1 Wb

  1. En una bobina de N = 400 espiras se produce un flujo total de 25 Wb cuando pasa por ella una corriente de 12 A. Calcular la energía magnética que almacena.

Solución: WB = 150 J.

  1. Una espira de alambre de 0,5 m2 de área está dentro de un campo magnético uniforme B = 2·10-2 T. Calcular el flujo que atraviesa la espira: a) cuando está colocada perpendicular al campo; b) cuando forma el plano de la espira con el campo un ángulo de 60º.

Solución: F = 0,01 Wb; F´= 9 mWb

  1. Una bobina plana de N = 200 espiras y radio r = 8 cm se coloca perpendicularmente a las líneas de fuerza de un campo magnético uniforme B = 0,8 T. Calcular la f.e.m. inducida en la bobina, si en 0,2 s: a) se anula el campo magnético; b) la bobina gira un ángulo de 90º; c) si gira, 180º. Indicar en un esquema el sentido de la corriente inducida en los casos a) y c).

Solución: e1 = 16,08 V; e2 = 16,08 V;  e3 = 32,16 V.

  1. En un campo magnético uniforme B, que varía sinusoidalmente, B = 0,2 sen wt, hay una bobina plana de N = 100 espiras y radio R = 4 cm. El eje de la bobina forma un ángulo de 60º con la dirección del campo B; calcular la f.e.m. inducida. Dato: frecuencia angular, w = 25 p rad/s.

Solución: e = -3,95 cos25pt V.

  1. Una bobina plana cuadrada de 10 espiras y de lado l = 12 cm gira con velocidad angular constante en un campo magnético uniforme B = 3 T. Se pide: a) dibujar la dirección del plano de la bobina relativa al campo magnético para que la f.e.m. inducida sea máxima; b) en este caso, la amplitud de la f.e.m. inducida es de 2,4 V; ¿cuánto vale la velocidad de rotación?; c) si se cierra la bobina, hallar la potencia media que se disipa en ella si tiene una resistencia de R = 0,2 W.

Solución: w = 5,56 rad/s ; P = 14,4 W

  1. Una varilla metálica de 2 m de longitud se desplaza con velocidad v constante y perpendicular a su eje sobre un plano horizontal. La componente vertical del campo magnético terrestre tiene la intensidad B = 4·10-5 T y aparece entre los extremos de la varilla una diferencia de potencial de 2 mV. Calcular la velocidad v.

Solución: v = 25 m/s

  1. Un solenoide largo de 15 espiras/cm (primario) está enrollado a un núcleo de hierro de 3 cm de diámetro. La permeabilidad magnética relativa del hierro es mr = 50. Otro solenoide (secundario) de 1.000 espiras se enrolla en la parte central del primario. Calcular el valor de la f.e.m. inducida en el secundario cuando se reduce a cero en 0,1 s la corriente de 2 A que pasa por el primario.

Solución: e = 1,34 V.

  1. Una varilla de masa m = 140 g y longitud L = 30 cm descansa en una superficie horizontal y pasa por ella una corriente de intensidad I = 12 A. Cuando se aplica un campo magnético vertical de B = 1,3·10-2 T la varilla empieza a deslizarse por la superficie. Determinar: a) el coeficiente estático de rozamiento entre la varilla y la superficie; b) el trabajo que realizan las fuerzas M campo magnético para desplazar la varilla, d = 1 m; c) el aumento de energía cinética en ese desplazamiento si el campo magnético se hace 3 veces más intenso.

Solución: ms =3,4·10-2 ; W1 = 4,68·10-2 J ; Eo = 9,36·10-2 J.

  1. Un carrete plano, de espesor despreciable, tiene 50 espiras y 100 cm2 de área por espira; está situado inicialmente de forma que su plano es perpendicular a un campo magnético uniforme y estático de 0,1 T. Se le hace girar después a una velocidad de 10 vueltas por segundo alrededor de un eje contenido en su plano y perpendicular al campo magnético. Hallar la f.e.m. inducida en función del tiempo.

Solución: e = 3,14sen20pt V.

  1. La densidad de energía magnética por unidad de volumen se expresa por la ecuación:

Si circula por un solenoide de 2.000 espiras una corriente de I = 10 A, y tiene en su interior un flujo de 10 Wb, calcular la energía magnética total que encierra el solenoide.

Solución: WB = 100 kJ

  1. Un circuito alimentado por una batería de f.e.m. e = 12 V y resistencia interior despreciable, contiene en serie una bobina de coeficiente de autoinducción L = 0,08 H y la resistencia R = 50 W. Calcular: a) la intensidad de la corriente en el instante en que se pierde en la resistencia la mitad de la potencia del generador; b) la rapidez con que aumenta la intensidad.

Solución: I = 0,12 A; dI/dt = 75 A/s.

  1. En bobinas de superconductores con corrientes elevadas se obtienen densidades de corrientes magnéticas de 10 MJ de energía por m3. Se pide: a) demostrar que la densidad de energía magnética por unidad de volumen es:   ; b) el campo magnético en el interior de las bobinas de superconductores; c) comprobar que dicho campo se mide en teslas.

Solución: B = 5 T.

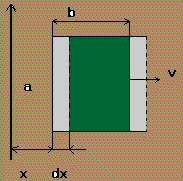  1. Una espira rectangular de lados a = 4 cm y b = 3 cm se separa con velocidad v = 0,2 m/s de un conductor rectilíneo indefinido por el que pasa una corriente I = 4 A. Si la espira se desplaza en el plano del hilo permaneciendo siempre paralelos a él los lados a, calcular la f.e.m. inducida si la distancia inicial del lado a al conductor es de x = 2 cm.

    Solución: e = 0,1 m


  1. En el problema anterior suponemos que circula una corriente variable en el tiempo,

i= 4-0,2t por el conductor rectilíneo indefinido. Calcular la f.e.m. inducida en la espira rectangular, si el lado a dista del conductor, d = 0,10 m permanente (la espira no se mueve).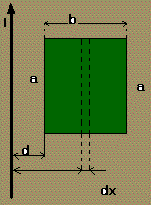

Solución: e = 0,42 nV.

 

 

volver página problemas