Problemas de movimiento ondulatorio.
- Un resorte lleva en un extremo una masa
m y oscila con un período T = 2 s. Si se aumenta la masa en 2 Kg, el nuevo
período es de 3 s. Calcular m.
Solución: m = 1,6 kg.
- El estudio experimental del movimiento
armónico simple de una partícula de 250 g se hace tomando t = 0 en el instante
en que pasa la partícula por el punto de equilibrio y de elongación negativa
a positiva. Si tarda 1 mín. 20 s en describir 100 oscilaciones completas,
y el valor máximo de la fuerza que produce el movimiento es F = 25 N, determinar:
A, w y jo en la ecuación
del movimiento: x = A cos (wt + j0).
Solución: A = 1,6 m; w =2,5 p rad/s; j0 = 1,5 p rad.
- Una bola de masa m = 20 g oscila con m.a.s.
con período T = p s y amplitud de
10 cm. Calcular: a) la velocidad máxima de la bola; b) la velocidad cuando
la fase es de 60º; c) la fuerza restauradora sobre la bola, cuando las fases
son: 0º, 30º y 90º respectivamente.
Solución: vmax = 0,20 m/s; v = 0,1 m/s; F1
= 0; F2 = -4·10-3
- Una partícula de masa 2 unidades SI se
mueve a lo largo del eje X hacia el origen, por la acción de una fuerza F
= -10 x i. Inicialmente está a 2 m del origen moviéndose con una velocidad
de 10 m/s. Calcular: a) el período del movimiento; b) el instante que pasa
por el origen la primera vez; c) la velocidad en dicho instante.
Solución:T
= 2,81 s; t = 0,19 s; v = -10,98 m/s
- Una partícula de masa 5 g oscila por la
acción de un resorte cuyo movimiento es: x = 7 cos(3t + 1), siendo x, cm;
t, segundos y 1 radianes. Determinar: a) la velocidad vm y la aceleración
am (máximas) de la partícula; b) el período de oscilación y la
constante recuperadora del resorte; c) los instantes en los que v y a se hacen
máximas; d) la representación gráfica de la aceleración instantánea en función
de la velocidad v y la de la aceleración a en función de la posición x.
Solución: vm = -0,21 m/s; am
= - 0,63 m/s2 ; T = 2,1 s; k = 45·10-3 N/m; t0 = 0,19
s; t1= 1,24 s...(v); t´1 = 0,71 s…(a)
- Un muelle elástico de 10 cm tiene uno
de sus extremos fijo en la pared vertical y descansa en una superficie horizontal
sin rozamiento. Se le aplica una fuerza de 20 N para mantenerlo estirado una
longitud de 15 cm. En esta posición se suelta y oscila libremente. Calcular:
a) la constante de recuperación del resorte; b) la ecuación del movimiento
vibratorio armónico resultante; c) las energías potencial EP y
cinética EC cuando x = 2 cm; d) velocidad máxima y aceleración
máxima en ese punto, indicando las elongaciones de cada una. Periodo de la oscilación 4 segundos
Solución: k = 400 N/m;
x = 0,05 sen ( 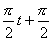 )m; Ep = 0,08 J ; Ec = 0,42 J.
)m; Ep = 0,08 J ; Ec = 0,42 J.
- En el centro de una piscina de 6 m de
radio se produce una perturbación que origina un movimiento ondulatorio en
la superficie del agua; la longitud de onda vale 3/4 m y tarda 12 s en llegar
a la orilla; calcular: a) el período y la frecuencia del movimiento; b) la
amplitud, si al cabo de 1/4 de segundo la elongación es de 4 cm; c) la elongación
de un punto situado a 6 cm del foco emisor en el instante t = 12 s.
Solución: T = 1,5 s;
f = 0,67 Hz; A = 4,62 cm; y = -2,23 cm.
- 1) Una cuerda de longitud L = 60 cm tiene
el extremo S unido a un vibrador animado de movimiento vertical sinusoidal
de amplitud A = 1,0 cm y frecuencia f = 100 Hz. El otro extremo está unido
a un dispositivo que impide la reflexión de onda. Si en el instante t = 0
el extremo S está en su posición de equilibrio y considerando positivo el
desplazamiento ascendente, deducir la ecuación de la elongación de S en función
del tiempo. 2) Las vibraciones se propagan con velocidad v = 30,0 m/s. Determinar:
a) la longitud de onda; b) el vector de onda k; c) la expresión de la elongación
de un punto M situado a una distancia x = 45,0 cm del punto S
Solución:
1) y = 1,0 sen 200p t cm;
2) l = 0,30 m; k = 20,9 m-1;
y = 1,0 sen ( 200pt – 9,4) cm.
- Una onda de 10 cm de amplitud se propaga
de izquierda a derecha y su período es de 12 s. Supuesta sinusoidal, hallar
la elongación en el origen cuando el tiempo es 1 s, contado a partir de la
iniciación del movimiento, desde la posición de equilibrio. En ese mismo instante,
la elongación es nula en un punto distante 4 cm del origen hacia la derecha.
Hallar la longitud de onda correspondiente.
Solución: y = 5 cm; l = 0,48 m.
- Una onda longitudinal se propaga por un
resorte que tiene un extremo unido a una fuente vibrátil. Si la frecuencia
de la vibración es f = 25 Hz y la longitud de onda, l = 0,24 m, calcular:
a) la velocidad de propagación; b) la ecuación de la onda, si la elongación
máxima es 0,3 cm y se propaga en sentido positivo en el eje OX.
Solución: v = 6 m/s ; y =
0,3·10-2 sen (50p - 26,18x) m.
- La
ecuación del movimiento de una onda transversal por una cuerda tensa es: y
= 0,25 cos (0,05 t - 0,2 x) en unidades SI. Calcular: a) la velocidad de
propagación de la onda por la cuerda; b) la velocidad del punto de la cuerda
x = 2,5 m en el instante t = 10 s.
Solución: v = 0,25 m/s;
v´ = 0.
- Una onda unidimensional se propaga de
derecha a izquierda con velocidad de 8 m/s, frecuencia f = 2 Hz y de amplitud
30 cm. Calcular: a) la longitud de onda; b) la ecuación de la onda; c) la
velocidad de una partícula en x = 2 m en el instante t = 1s.
Solución:l
= 4 m; y = 0,30 sen (4pt + 1,57x) m.; v = -3,77 m/s
- Una
cuerda puesta en el eje OX vibra transversalmente según el eje 0 Y con movimiento
ondulatorio de ecuación: y(x, t) = 0,002 sen (60 x + 300 t) en unidades SI.
Se pide: a) dirección y velocidad con que se propaga la onda; b) longitud
de onda y frecuencia del movimiento.
Solución: v = -5 m/s; l = 0,10 m; f = 47,75 Hz.
- Dos ondas de ecuaciones: y1
= 6 sen (1.500 t – 250 x) y2
= 6 sen (1.500 t + 250 x) en
unidades SI, interfieren. Calcular: a) la ecuación de las ondas estacionarias
resultantes; b) la amplitud de los nodos; c) la distancia entre dos vientres
consecutivos.
Solución: a) y = 12 cos
250 x · sen 1,500t; b) y = 0; c) d = 1,26·10-2 m.
- El extremo de una cuerda
x = 0, oscila según la ecuación: y = A sen wt, siendo A = 0,1 m y
w
= 20p rad/s. Por la cuerda se propaga una onda sinusoidal,
y el punto x1 = 0,05 m vibra según la expresión y = A sen (wt
- p/4).
Calcular: a) la frecuencia de la onda; b) la velocidad
de propagación; e) la longitud de onda; d) la ecuación de la onda.
Solución:
f = 10 Hz; v = 4 m/s; l = 0,4 m; y = 0,1 sen 2p(t/0,1 - 5x/2) m.
- Una onda armónica esférica tiene de intensidad
6·10-8 W/cm2 a 20 m del foco emisor. Si no hay absorción,
calcular: a) la energía emitida por el foco emisor en un minuto; b) la amplitud
de la onda a los 40 m, si a los 20 m es de 4 mm.
Solución: E = 180,96
J; A2 = 2 mm.
- Una perturbación se propaga
por un medio elástico, según la ecuación: y
= 24 sen (1.987 t – 6 x) en unidades SI. Determinar: a) la frecuencia de las
vibraciones; b) la velocidad de propagación de la onda; c) la ecuación de
otra onda que se propaga en sentido contrario, e idéntica a la dada.
Solución: f = 316,2
Hz; v = 331 m/s; y = 24 sen (1.987t + 6x) m.
- a) Calcular la velocidad del sonido en
hidrógeno a 27ºC si la del sonido en el aire a 0ºC es de 331 m/s; b) Hallar
la longitud de onda del sonido cuya frecuencia es de 435 Hz. El valor de l en aire a 15ºC
Solución: v = 1,317,4 m/s; longitud de onda = 3 m/s; v15 = 340 m/s
- Una cuerda vibra según la ecuación: y(x,
t) = 5 sen (1/3)·p·x cos 40 p·t ( estando x e
y en cm, t en segundos) Calcular: a) la amplitud y velocidad de las ondas
que originan la onda estacionaria; b) la velocidad en un punto que dista x
= 1,5 cm del origen en el instante t = 1,25 s; c) la distancia entre dos nodos.
Solución:a) y = 2A sen kx cos wt; w = 40 p ; k= p/3; v=1,20 m/s;c) 3 cm
- En una cuerda horizontal de longitud indefinida
se produce una onda sinusoidal transversal en x = 0; el movimiento de la misma
se produce dos veces cada segundo. Si la densidad lineal de la cuerda es de
0,25 kg/m y está sometida a una tensión de 10 N, calcular: a) la velocidad
de propagación del movimiento ondulatorio en la cuerda; b) la frecuencia y
longitud de onda del mismo; c) la ecuación del movimiento; d) la velocidad
y aceleración de un punto situado a 3,16 m del origen de la perturbación.
Dato: amplitud del movimiento, A = 0,5 m.
Solución: v = 6,32 m/s; f=
2 Hz; l = 3,16 m; y = 0,5 sen 2p(t/0,5
- x/3,16)m;
vx = 2p cos(4pt – 6,32) m/s; ax = -8 p2 sen (4pt – 6,32) m/s2
- Dos masas de 0,80 y 1,0 kg penden de resortes
idénticos de constante elástica k = 4,0·p2 N/m. Ambos se
sueltan para oscilar simultáneamente de sus desplazamientos máximos iguales
y describen m.a.s. Calcular: a) las frecuencias de oscilación de cada uno
de ellos; b) el menor tiempo en que uno de ellos da exactamente una vibración
más que el otro (período de las pulsaciones); c) la frecuencia con que ambos
resortes alcanzan en el mismo instante la elongación máxima (frecuencia de
las pulsaciones).
Solución: f1
= 1,12 Hz; f2 = 1 Hz; T = 8,3 s; fp = 0,12 Hz
- La
ecuación de una onda en unidades SI es: y = 0,04 sen (30Opt - 3x) Calcular:
a) la frecuencia de la onda y su velocidad; b) la diferencia de fase entre
las posiciones de un punto en el intervalo de tiempo t = 1 s; e) la distancia
entre dos puntos consecutivos cuya diferencia de fase es p/3 radianes; d) la diferencia de fase entre dos puntos, en un instante
dado, cuya separación es de 0,5 m.
Solución:
f = 150 Hz; v = 315 m/s; Dj = 300 p rad; Dx = 0,35 m; Dj = 1,5 rad
- La emisora de radio A emite con frecuencia
de 30 M Hz; y la B, con frecuencia de 300 M Hz. Si se admite que la intensidad
de ambas es la misma y no hay amortiguamiento, calcular: a) sus longitudes
de onda; b) la relación de sus amplitudes en un punto equidistante de ambas;
¿qué emisora llega con mayor amplitud?
Solución: l1 = 10 m; l2 =1 m; A2 = 0,10
A1
- Una
onda sonora plana, sin amortiguamiento, se propaga en un medio gaseoso con
velocidad v = 350 m/s en la dirección OX; la frecuencia de la onda armónica
es de 12 k Hz y la amplitud de la oscilación de la molécula del medio, 3·10-5
m. Si la elongación en el instante inicial es de 1,5·10-5 m en
el punto (0, 0, 0), a) calcular la longitud de onda; b) deducir la ecuación
de la onda sonora.
Solución: l = 2,9·10-2 m; y(x,t)
= 3·10-5 sen (24p·103t – 216,67 x + p/6)m
- En el punto M se superponen dos movimientos
ondulatorios procedentes de dos focos coherentes A y B. La distancia M A es
35 m y la M B, 20 m. Se propagan con velocidad de 900 m/s y frecuencia, 150
Hz. La amplitud del movimiento ondulatorio procedente de A es 0,4 m en el
punto M, y la procedente de B, 0,3 m. Determinar: a) la función del movimiento
que define el estado del punto M; b) la relación de intensidades entre la
del movimiento ondulatorio en M y las de cada movimiento que incide en M procedentes
de A y B.
Solución: y = 0,7 sen (300pt - 1,11)m; I/I1 = 3; I/I2 = 5,4
- Se emite un sonido de 80 dB y frecuencia
de 2.000 Hz. Calcular la longitud de onda y la intensidad sonora si se supone
para temperatura del aire 15 ºC.
Solución: l = 0,17 m; I = 10-4
W/m2
- Un observador recibe dos sonidos producidos
simultáneamente cuyos niveles de intensidad sonora son 40 y 60 dB. Calcular:
a) la intensidad del sonido resultante; b) el nivel de intensidad sonora del
mismo
Solución: I
= 1,01·10-6 W/m2
- Un tren pasa por un puente a 105 km/h
y emite un sonido de 530 Hz. Calcular la frecuencia que percibe un observador
situado cerca de la vía, al acercarse el tren y al alejarse; velocidad del
sonido, 340 m/s.
Solución: f1
= 580 Hz; f1` = 488 Hz.
- Un coche se separa de una pared a 90 km/h
y se dirige hacia un observador emitiendo un sonido de 600 Hz. Calcular: a)
la frecuencia que llega al observador directamente; b) la que le llega después
de reflejarse en la pared.
Solución: f1
= 647,6 Hz; f1` = 559 Hz.
- Si en el problema anterior soplara un
viento de 30 m/s en la dirección y sentido del movimiento del coche, deducir
las frecuencias que percibe el observador: a) directamente del coche; b) después
de reflejarse en la pared.
Solución: f1
= 704,8 Hz; f1` = 555 Hz.
volver
página problemas
![]() )m; Ep = 0,08 J ; Ec = 0,42 J.
)m; Ep = 0,08 J ; Ec = 0,42 J.