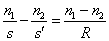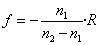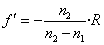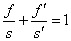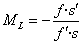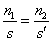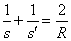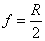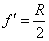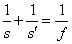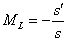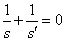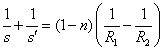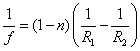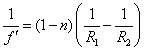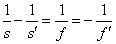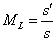Resumen de las relaciones más importantes de dioptrios, espejos y lentes.
|
|
Fórmula Fundamental |
Foco objeto |
Foco imagen |
Fórmula General |
Aumento Lateral |
|
Dioptrios esféricos |
|
|
|
|
|
|
|
|||||
|
Dioptrios planos |
|
|
|
|
|
|
Espejos esféricos |
|
|
|
|
|
|
|
|||||
|
Espejos planos |
|
|
|
|
|
|
Lentes |
|
|
|
|
|
|
|
|||||
ÓPTICA GEOMÉTRICA. DIOPTRIOS: ESPEJOS Y LENTES
1. ¿Cuál ha de ser el índice de refracción de una esfera transparente para que los rayos paraxiales procedentes del infinito se concentren en el vértice de la segunda superficie?
Resultado: n = 2
2. Una varilla larga de vidrio (n = 1,50) de 8 cm de diámetro termina en su extremo en una superficie semiesférica de 4 cm de radio. La varilla se sumerge en un líquido. Un objeto situado sobre el eje de la varilla a 60 cm del extremo forma su imagen en un punto situado 100 cm dentro de la varilla. ¿Cuál es el índice de refracción del líquido?
Resultado: n = 1,35
3. Un haz estrecho de rayos paralelos penetra en dirección radial en una esfera de vidrio (n = 1,50) maciza, de 3 cm de radio. ¿En qué punto fuera de la esfera se reúnen estos rayos?
Resultado: A 1,5cm de la esfera
4. Una esfera de vidrio de paredes delgadas y radio A está llena de agua. A una distancia 3R de su superficie se coloca un objeto. Hallar la posición de la imagen final.
Resultado: A una distancia 4R del centro de la esfera
5. ¿Cómo ha de ser un objeto para que mediante un espejo esférico convexo se obtenga de él una imagen real?
6. Una varilla de vidrio (n =1,5) termina en sus extremos en dos semiesferas de 5cm de radio. Al situar un objeto sobre el eje de la varilla ya 20 cm de un extremo, la imagen final se forma a 40 cm del extremo opuesto. Hallar la longitud de la varilla.
Resultado: L = 50 cm
7. Si delante de un espejo esférico podemos vernos en cualquier posición en la que nos situemos, ¿de qué clase de espejo se trata? ¿Y si a cierta distancia la imagen desaparece?
8. ¿Cuáles son los puntos conjugados del foco objeto y del foco imagen?
9. Se dispone de un espejo cóncavo de 20cm de radio y se desea que la imagen se forme a 1 m del espejo. ¿A qué distancia se deberá colocar el objeto?
Resultado: s = 1/9 m
10. Un objeto se encuentra a 15 cm de distancia del centro de un vidrio esférico de 3 cm de radio que adorna un árbol de Navidad. ¿Cuál es el aumento de la imagen?
Resultado:
ML = 0,2
11. La distancia focal de un espejo cóncavo es 0,2 m. ¿Cuánto mide su radio de curvatura? ¿A qué distancia se formará la imagen si el objeto está situado a 2 m del espejo?
Resultado: s´ = - 0,22 m
12. ¿A qué distancia de un espejo convexo de 30 cm de distancia focal habrá que colocar un objeto de 2 cm de altura para que su imagen tenga una altura de 4 cm?
Resultado: s = -30 cm
13. Sobre una pantalla se desea proyectar, mediante un espejo esférico cóncavo que dista de ella 10 m, la imagen de un objeto, de modo que resulte un aumento igual a 4. Determinar la distancia del espejo a la que se debe colocar el objeto, así como el radio de curvatura del espejo.
Resultado: s = -2,5 m; R = 4 m
14. Un espejo esférico cóncavo, para afeitarse, tiene un radio de curvatura de 30 cm. ¿Cuál es el aumento lateral del espejo cuando el rostro del observador está a 10 cm del vértice del espejo?
Resultado: ML = 3
15. Demuestra mediante un dibujo cuál es el tamaño mínimo de un espejo plano vertical, en el cual un observador pueda ver su imagen completa.
16. Calcular la profundidad aparente de una piscina de agua (n = 1,33) de 2 m de profundidad cuando se la mira verticalmente al fondo desde el aire.
Resultado: s’=1,5 m
17. ¿A qué distancia de una lente convergente se ha de colocar un objeto para que su imagen sea de igual tamaño?
18. ¿Varía la distancia focal de una ente si se invierte su orientación respecto al sentido de propagación de la luz? Razona la respuesta.
19. Por medio de una lente se forma la imagen real de un foco luminoso puntual. ¿Qué rayos llegan antes a la imagen: los que pasan por el centro de la lente o los que la atraviesan por las zonas cercanas al borde? Justifica razonadamente tu respuesta.
20. En un cine se desea aumentar el tamaño de a imagen proyectada sin modificar las dimensiones de la sala y para lograrlo se cambia el objetivo del proyector. ¿Cómo ha de ser la distancia focal del nuevo objetivo: mayor o menor que la del anterior?
21. Con una lente convergente se obtiene una imagen real a 5 cm de la lente si el objeto está situado a 25 cm de la lente. Calcular la distancia focal imagen.
Resultado; f´ = 4,17cm
22. Se coloca un objeto a 36cm de una pantalla.
a) ¿En qué puntos entre el objeto y la pantalla ha de colocarse una ente de 8 cm de distancia focal para obtener una imagen sobre la pantalla?
b) ¿Cuál es el aumento de la imagen para estas posiciones de la lente?
Resultados:
a) A 12 cm y a 24 cm del objeto;
b) ML = -2; ML´ = -1
23. Una lente biconvexa delgada, de radios de curvatura iguales a 12 cm y de 8,33 dioptrías de potencia, proyecta sobre una pantalla una imagen de tamaño 20 veces mayor que el del objeto. Determinar a qué distancia de la lente es necesario colocar el objeto y la pantalla, así como el índice de refracción de la lente.
Resultado:
El objeto a 12,6cm y la pantalla a 2,52 m; n = 1,5
24. Una tente biconvexa delgada, cuyas caras tienen radios de curvatura de 20 cm, está situada a 25 cm de una pantalla. Si lleva acoplada una lente planocóncava, de índice de refracción 1,5, el sistema forma sobre la pantalla a imagen del infinito del eje. Si se quita a segunda lente, para que la imagen se siga formando en la pantalla es necesario aproximar ésta 8,34 cm. Calcular el índice de refracción de la primera lente, las potencias de ambas lentes y el radio de curvatura de la cara cóncava de la segunda.
Resultados: n = 1,6; C1 = 6 dioptrías; C2 = - 2 dioptrías; R = 25 cm
25. Analiza las distintas aberraciones que pueden presentar las lentes, así como las distintas maneras de corregirlas. ¿Qué importancia presentan estas aberraciones? ¿A qué son debidas?