DINÁMICA SISTEMA DE PARTÍCULAS

1.- Se lanza un objeto de masa m con velocidad v, sobre un carro de masa M en reposo que puede rodar libremente. Llega un momento en que m y M se mueven juntos siendo el espacio recorrido por el carro mientras el bloque desliza sobre él S. Calcular el coeficiente de rozamiento entre ambos. ¿Qué espacio ha recorrido el objeto ?. Hallar la variación de Energía cinética del sistema formado por los dos cuerpos y el trabajo de las fuerzas interiores al sistema.

2.- Un carro repleto de arena, de masa M, se mueve con velocidad v0 sobre una superficie horizontal. Una partícula de masa m se mueve con velocidad v en sentido contrario a v0. y choca contra el carro incrustándose. Debido al golpe el carro retrocede y se mueve una distancia d hasta que se para. Si m es el coeficiente de rozamiento entre el suelo y carro. Hallar el valor de v.

3.- Dos partículas de masa m cada una están unidas por una varilla de masa despreciable y giran en un plano horizontal con velocidad w₀ alrededor de un eje que pasa por el centro de la varilla. Se coloca otra masa de valor M = 3 m de modo que se produce el choque quedando unidas las dos masas. Hallar la variación del momento lineal y de la energía cinética del sistema durante el choque.

4.- Se deja caer una bola de masa m desde una altura de H = 1,6 m sobre un plano inclinado que forma 30º con la horizontal. La bola choca con el plano siendo el coeficiente de restitución e= 3/4. Hallar el lugar donde volverá a chocar la bola sobre el plano inclinado.

5.- Dos partículas de masas m_l y m₂ (m_l = 2m₂) están unidas como indica la figura por un muelle de constante K y longitud natural despreciable. Ambas están separadas una distancia d y pueden deslizar libremente, sin rozamiento, por dos raíles paralelos. Si inicialmente a = 45º, ¿cuál será su velocidad cuando estén en la situación 2 de la figura

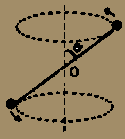6.- La varilla de la figura, de masa despreciable y longitud d se encuentra fija en 0, siendo j el ángulo que forma con el eje Z. En sus extremos hay dos objetos puntuales de igual masa m, que describen un movimiento circular de w constante. Hallar momento angular del sistema respecto a 0, respecto a Z, y el valor de la fuerza de reacción en O

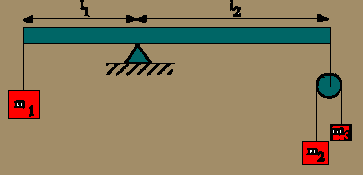7.- Calcular la relación entre las masas y la longitud del sistema de la figura para que la viga, de masa despreciable, se encuentre en equilibrio.

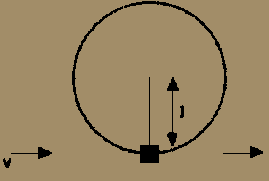8.- Una bala de masa m y velocidad v pasa a través del cubo de un péndulo de masa M saliendo con una velocidad v/2. El choque se considera instantáneo. El cubo cuelga del extremo de una cuerda de longitud l. ¿Cuál es el menor valor de v para el cual el péndulo completará la circunferencia entera?