HIDRODINÁMICA

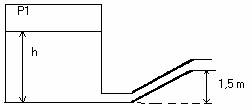
1. Un recipiente de paredes verticales esa lleno de un líquido hasta una altura h. Calcular el alcance de dos chorros que provienen: uno de abrir un orificio a una altura “y” de la superficie y otro de abrir un orificio a una altura “y” del fondo.

2. Un gran depósito de agua tiene unida una tubería como indica la figura. El depósito está cerrado en la parte superior y contiene aire comprimido entre la superficie del agua y de la tapa. Cuando la altura del agua es h₂= 3m la presión manométrica es de 2.4·10⁵ Pa. ¿ Cuál es la velocidad de salida del agua por la manguera ?

3. Hallar el caudal de agua en el venturímetro de la figura a través de la lectura entre la diferencia de alturas del mercurio. D₁ = 15 cm.  D₂ = 30 cm

r_mercurio = 13.6 g /cm³

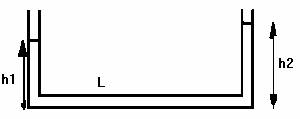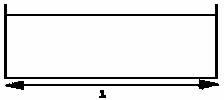
4. Un tubo en U de longitud 1 contiene líquido. ¿Cuál es la diferencia de alturas de líquido de las ramas verticales cuando el tubo tiene una aceleración a hacia la derecha?

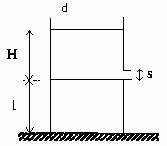
5. Calcular en el depósito cúbico de la figura, las fuerza de reacción normales al suelo que reciben los soportes en el instante señalado. H = 5m , r = 1000 Kg./m³, d = 2 m,    l= 6 m, s«S; s = 10 cm².

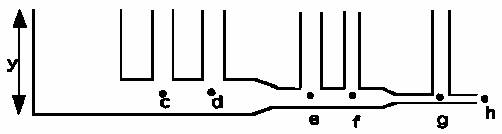
6. El depósito de la figura está abierto a la atmósfera, tiene una sección muy grande y una altura y = 40 cm. las secciones transversales de los tubos horizontales son: 1 cm², 0,5 cm² y 0,2 cm². Si el tubo h está abierto a la atmósfera, ¿Cuál es el volumen de líquido por unidad de tiempo que sale del depósito, la velocidad en cada porción de tubo horizontal y las alturas de los líquidos en los tubos verticales?

7. Obtener la forma que adquiere la superficie del líquido cuando: a) se mueve hacia la derecha con aceleración a, b) gira con velocidad constante w en torno a un eje que pasa por su centro.

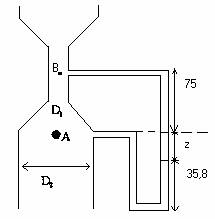
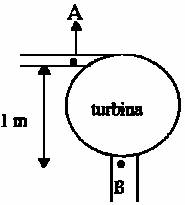8. Obtener la potencia comunicada por la corriente de agua, de caudal 0,214 m³/s, a la turbina si la presión manométrica de A es 147,5 kPa, la de B es -34,5 kPa y los diámetros son 300 mm y 600 mm.