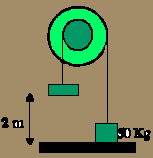
 Dos
poleas del mismo eje y radios 50 y 80 cm están unidas formando una poleade
momento deinercia I=72 Kg.·m2. De los hilos, de masa despreciable,
penden dos masas de 100 y 50 Kg., dejándose libre el sistema en la posición
de la figura. Hallar la velocidad del cuerpo de 100 Kg. al llegar al suelo
y la altura total recorrida por el cuerpo de 50 Kg. hasta llegar que se
para. Verificar si se conserva la energía mecánica del sistema.
Dos
poleas del mismo eje y radios 50 y 80 cm están unidas formando una poleade
momento deinercia I=72 Kg.·m2. De los hilos, de masa despreciable,
penden dos masas de 100 y 50 Kg., dejándose libre el sistema en la posición
de la figura. Hallar la velocidad del cuerpo de 100 Kg. al llegar al suelo
y la altura total recorrida por el cuerpo de 50 Kg. hasta llegar que se
para. Verificar si se conserva la energía mecánica del sistema.
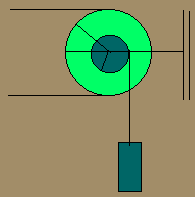 2.
La figura representa dos poleas acopladas de momento de inercia I = 200
Kg.·m2. Los radios son R1 = 10 cm, R2 = 20 cm. Calcular
la diferencia de tensiones en las cuerdas horizontales cuando el bloque
de 500 Kg.:
2.
La figura representa dos poleas acopladas de momento de inercia I = 200
Kg.·m2. Los radios son R1 = 10 cm, R2 = 20 cm. Calcular
la diferencia de tensiones en las cuerdas horizontales cuando el bloque
de 500 Kg.:
a) sube a velocidad constante
b) Baja con aceleración de 0,2 m/s2 (tomar g = 9,8 m/s2)
 La barra de la figura, de masa M y longitud L está sujeta inicialmente a
un hilo y a un soporte en C. Se rompe el hilo. Hallar en ese instante:
La barra de la figura, de masa M y longitud L está sujeta inicialmente a
un hilo y a un soporte en C. Se rompe el hilo. Hallar en ese instante:
a) aceleración del punto B
b) Fuerzas en C
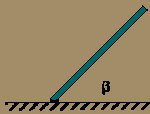 Una
varilla homogénea de longitud L y una masa M se deja en libertad partiendo
del reposo cuando b
= 60º. Suponiendo que el rozamiento entre elextremo y el suelo es lo suficientemente
grande para evitar todo deslizamiento calcular:
Una
varilla homogénea de longitud L y una masa M se deja en libertad partiendo
del reposo cuando b
= 60º. Suponiendo que el rozamiento entre elextremo y el suelo es lo suficientemente
grande para evitar todo deslizamiento calcular: a) aceleración angular de la varilla en el instante de soltarla.
b) Reacción perpendicular y paralela y paralela al suelo en el punto de contacto de la barra con el suelo en dicho instante.
 Un carrete de radio interior
r y exterior R está situado sobre una superficie plana. Se tira del carrete
con una fuerza F que forma un ángulo j con la horizontal haciendo
que ruede sin deslizar. Hallar el valor del ángulo j0
para el cual el carrete gira a izquierdas.
Un carrete de radio interior
r y exterior R está situado sobre una superficie plana. Se tira del carrete
con una fuerza F que forma un ángulo j con la horizontal haciendo
que ruede sin deslizar. Hallar el valor del ángulo j0
para el cual el carrete gira a izquierdas.
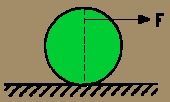 Hacer un estudio del valor de la fuerza de rozamiento en función del punto
de aplicación de la fuerza F, para el cilindro de la figura de masa m y
radio r, si la fuerza aplicada es paralela al suelo y de sentido el de la
figura y el sistema rueda sin deslizar.
Hacer un estudio del valor de la fuerza de rozamiento en función del punto
de aplicación de la fuerza F, para el cilindro de la figura de masa m y
radio r, si la fuerza aplicada es paralela al suelo y de sentido el de la
figura y el sistema rueda sin deslizar.
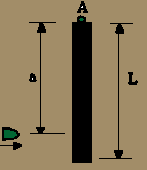 Una varilla de longitud L y masa M puede rotar libremente alrededor de un
pivote A. Una bala de masa m y velocidad v golpea a la varilla a una distancia
a del punto A y se incrusta.
Una varilla de longitud L y masa M puede rotar libremente alrededor de un
pivote A. Una bala de masa m y velocidad v golpea a la varilla a una distancia
a del punto A y se incrusta.
a) Hallar la velocidad angular del sistema inmediatamente después de que la bala golpee a la varilla.
b) Bajo que condiciones se conserva el momento lineal durante el choque.
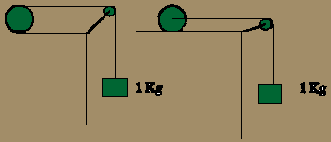 Una
masa de 1 Kg. cuelga del extremo de una cuerda sin masa, que pasa por una
polea si rozamiento y después se acopla a un cilindro de masa 8 Kg. y radio
10 cm que rueda sin deslizar. Hallar la aceleración del cuerpo que cuelga,
la tensión de la cuerda y la aceleración angular del cilindro.
Una
masa de 1 Kg. cuelga del extremo de una cuerda sin masa, que pasa por una
polea si rozamiento y después se acopla a un cilindro de masa 8 Kg. y radio
10 cm que rueda sin deslizar. Hallar la aceleración del cuerpo que cuelga,
la tensión de la cuerda y la aceleración angular del cilindro.
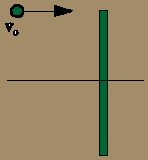 Sobre
un plano horizontal, sin rozamiento, se produce el choque que indica la
figura. La bola, de masa M y velocidad v0, queda adherida en
el extremo de la varilla. La varilla tiene longitud L y masa M. Describir
el movimiento del sistema después del choque.
Sobre
un plano horizontal, sin rozamiento, se produce el choque que indica la
figura. La bola, de masa M y velocidad v0, queda adherida en
el extremo de la varilla. La varilla tiene longitud L y masa M. Describir
el movimiento del sistema después del choque.
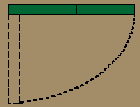
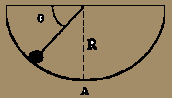 La esfera de la figura,
de radio R0 = R/10, y masa m rueda sin deslizar sobre la superficie
esférica. Si se suelta en el instante representado en la figura, hallar
la velocidad del centro de masas de la misma en A.
La esfera de la figura,
de radio R0 = R/10, y masa m rueda sin deslizar sobre la superficie
esférica. Si se suelta en el instante representado en la figura, hallar
la velocidad del centro de masas de la misma en A.
 Una varilla de 2 m de longitud está formado por dos materiales, de modo
que una mitad pesa 1 Kg. y la otra 2 Kg. Se suspende de un eje que pasa
por uno de sus extremos y se deja libre. Hallar la velocidad w
en su punto más bajo dependiendo de que el eje esté en uno u otro extremo.
Una varilla de 2 m de longitud está formado por dos materiales, de modo
que una mitad pesa 1 Kg. y la otra 2 Kg. Se suspende de un eje que pasa
por uno de sus extremos y se deja libre. Hallar la velocidad w
en su punto más bajo dependiendo de que el eje esté en uno u otro extremo.