Problema:

Perez andereñoa Ikasle Ona institutuko Natura irakaslea da. Bere laborategirako goitik irekita dauden zenbait kutxa behar ditu bere saiakuntzetarako erabiltzen dituen material desberdinak gordetzeko. Horretarako 60cm-ko aldedun metalezko xafla karratuak erosi ditu:
Xaflaren ertz bakoitzean karratutxo bat moztu eta erlaitzak goruntza tolestu ondoren bere hegaletatik itsasteko ideia du.
Bolumen handiena duen kutxa lortzeko zeintzuk dira ertzetan moztu beharreko laukitxoen neurriak?

 

LANERAKO GIDOIA
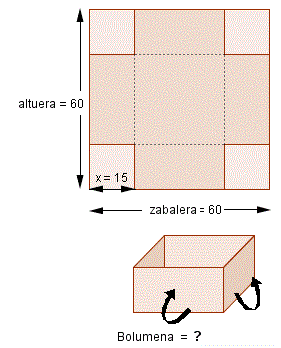  1. Irudia beha ezazu. Xafla metalikoen ertzetan 15cm-ko aldedun karratuak moztea erabakiko bagenu, zeintzuk izango lirateke kutxaren dimentsioak eta bolumena (litrotan) erlaitzak tolesterakoan.
  2. Zelan aldatuko lirateke dimentsio hoiek mozten ditugun karratuek 12cm-ko aldeak balituzte?
  3. Karratu txikiagoak moztuko bagenitu, bolumen handiagoko kutxak lortuko genituzke beti? Erantzuna azal ezazu
  4. Perez irakasleak ahalik eta bolumen handieneko kutxak lortu nahi dituenez, otutzen al zaizu bolumen handiena lortzeko moztu behar ditugun karratuen neurriak determinatzeko modurik?
  5. Kutxaren altuera ezagututa, hau da, moztutako karratuaren aldea (dm-tan) ezagututa, kutxaren bolumena (litrotan) emango digun adierazpen algebraikoa bila ezazu.
  6. Lortutako formulatik balio taula bat sor ezazu.
  7. Beheko irudi interaktiboa beha ezazu. Puntu berdea mugi ezazu eta balio taulan ea akatsik duen egiazta ezazu.
  8. Puntu gorriaren esanahia eta bere aldakuntza puntu berdea mugitzerakoan azaldu itzazu.
  9. Justifika edo ezezta itzazu ondoko baieztapenak, erantzuna arrazonatuz:
    a) Kutxaren bolumena handitu eta txikitu egiten da kutxaren altuera handitzerakoan.
    b) Ezinezkoa da kutxaren bolumena kalkulatzea bere hiru dimentsioetatik bat bakarrik ezagututa.
    c) Kutxaren altuera eta bolumenaren arteko erlazioa lineala da.

Lo sentimos, el applet Geogebra no pudo iniciarse.
Por favor, comprueba que la plataforma Java 1.4.2 (o posterior) está instalada y activada.
(Pulsa aquí para instalar Java ahora)

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

  1. 5. galderan definitutako funtzioa grafikoki adieraziko dugu: puntu gorriaren gainean eskuineko botoiarekin klika ezazu eta "trazoa aktibatu". Gero puntu berdea mugi ezazu. Gertatutako deskriba ezazu.
  2. Zein da funtzioaren izare eremua? Zergaitik?
  3. Grafikako zein puntutan hartzen da baliorik altuena? Konproba ezazu "Erantzuna ikusi" irristailuaren bidez.
  4. Nolakoa izango da grafikarekiko ukitzailea puntu horretan? Konproba ezazu "Ukitzailea ikusi" irristailuaren bidez.
  5. Zein izango da bere maldaren balioa? Zein da balio horren eta funtzioaren deribatuak puntu horretan duen balioaren arteko erlazioa?
  6. Har ezazu 5. galderan, bolumenarentzako definitutako funtzioa eta bere deribatu funtzioa kalkula ezazu.
  7. Bertan ordezka ezazu x-a, soluzioren balioagaitik. Zenbat ematen du?
  8. Zure ondorioak laburtu itzazu: nola lor daiteke funtzio baten balio maximo edo minimoa?

Optimizazio problemen adibide gehiago

Manuel Sada Allok (2006ko apirila) egokitua Lupiáñez, J.L. eta Codina, A. (2002)ren proposamenetik. Kalkulagailu grafikoarekin optimizazio problemak inplementatzen.Matemarikaren ikaskuntza eta irakaskuntzari buruzko X. kongresuan aurkeztutako lana. El Ejido, Almería.Jose Luis Lupiáñez Gómez eta Antonio Codina Sánchez-en jarduera batetik sortua.