Geometriako problema ala Progresioetakoa al da?
|
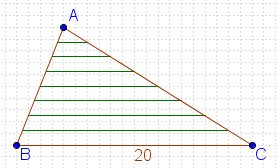
ABC triangeluan, BC zuzenkiarekiko paraleloak diren zazpi zuzenki irudikatu ditugu; zazpi zuzenki hauek AC aldea 8 zatitan banatzen dute. BC = 20 zentimetrotakoa bada, zein da 7 zuzenkien luzeren batura?
(Santiago Férnandezek Divulgamat-en proposatutakoa; Retos Matemáticos-etik hartua)
|
 |
- Beheko irudian nabegazio botoiak erabil itzazu, Geogebrarekin egindako eraiketa posible bat ikusteko. Triangeluaren erpinak mugitu ondoren, neurrietan gertatutako aldaketak beha itzazu.
- Gero, eskuineko leihoan eskura dituzun erremintak erabiliz, eraiketa hori errepikatzen saia zaitez.
|
|
- Noski, aurreko metodoa erabilgarria izan da, 7 zuzenki izateran (aldeak 8 zati berdinetan banatzen dituztenak), eraiketa egiterako orduan erdiko puntuak lagungarriak direlako. Baina 7 zuzenki izan beharrean 13 bagenitu, horrelako erraza izango litzateke?
Beste metodo bat bila dezagun: beheko irudian, irristailua (edo animazio botoia) erabili ondoren beha ezazu:
- Orokortzea: ondoko bi irudietan irristailuak erabili ondoren, gertatutako aldaketak beha itzazu eta progresio aritmetiko bateko elementuak batzeko erabiltzen den formula justifikatzen saia zaitez:
Zein da lehenengo 50 zenbaki arrunten arteko batura? Ondoko irudiaren antzeko zerbait izan liteke Gauss umeak kalkulua era arin batean egiteko imajinatuko zukeena?
Manuel Sada Allok GeoGebra -rekin egina (2009ko abuztua)
