Problema: La Srta. Pérez es profesora de Ciencias en el Instituto El Buen Estudiante. Para su laboratorio necesita varias cajas abiertas por arriba para almacenar los diferentes materiales que usa en sus experimentos, y ha comprado un buen número de láminas planas de metal para hacerlas. Cada lámina es un cuadrado de 60 cm de lado: La idea que tiene es cortar un cuadradito en cada esquina de una lámina, y doblar hacia arriba las pestañas pegándolas por su borde. ¿Podrías ayudar a la profesora Pérez a elegir las medidas del cuadradito que se recorta en las esquinas, con idea de obtener la caja con el mayor volumen posible?   GUIÓN DE TRABAJO

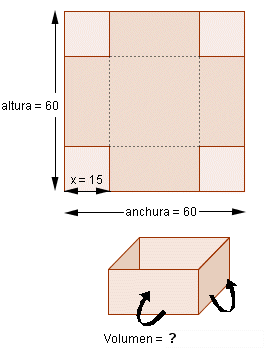1. Observa la figura. Si decidimos cortar cuadrados de 15 cm de lado en las esquinas de las láminas metálicas, determina las dimensiones y el volumen (en litros) que tendrá la caja que formaremos al doblar las pestañas.
2. ¿Cómo cambiarían esas dimensiones si los cuadrados que cortamos son de 12 cm de lado?
3. Si cortamos cuadrados más pequeños, ¿obtenemos necesariamente cajas de un volumen mayor? Explica tu respuesta
4. Como la profesora Pérez quiere obtener cajas con el volumen más grande posible, ¿se te ocurre alguna manera de determinar la medida del cuadrado que cortaremos para lograr ese mayor volumen?
5. Encuentra una expresión algebraica que permita conocer el volumen (en litros) de la caja a partir de su altura, es decir, del lado del cuadrado recortado (en dm).
6. Construye una tabla de valores a partir de la fórmula obtenida.
7. Observa la figura interactiva de debajo. Mueve el punto verde y comprueba si tienes errores en la tabla de valores.
8. Explica el significado del punto rojo y su variación al mover el verde.
9. Justifica o niega las siguientes afirmaciones, razonando tu respuesta:
   a) El volumen de la caja aumenta y disminuye al incrementar la altura de la caja.
   b) Es imposible hallar el volumen de una caja conociendo sólo una de sus tres dimensiones.
   c) La relación entre la altura de una caja y su volumen es lineal.

Lo sentimos, el applet Geogebra no pudo iniciarse.
Por favor, comprueba que la plataforma Java 1.4.2 (o posterior) está instalada y activada.
(Pulsa aquí para instalar Java ahora)

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

10. Vamos a representar gráficamente la función definida en la cuestión nº 5: haz clic derecho sobre el punto rojo y "activa la traza". Luego vuelve a mover el punto verde. Describe lo que ocurre.
11. ¿Cuál es el dominio de la función? ¿Por qué?
12. ¿En qué punto se alcanza el valor más alto de la gráfica? Compruébalo mediante el deslizador de "Ver solución"
13. Cómo será la tangente a la gráfica en ese punto? Compruébalo mediante el deslizador de "Ver tangente"
14. ¿Cuál será el valor de su pendiente? ¿Qué relación tiene ese valor con la derivada de la función en ese punto?
15. Toma la función definida en la cuestión 5 para el volumen y calcula su función derivada.
16. Sustituye en ella la x por el valor dado para la solución. ¿Cuánto da?
17. Resume tus conclusiones: ¿cómo se puede calcular el valor máximo o minimo de una función?

Más ejemplos de problemas de optimización

Adaptado por Manuel Sada Allo (Abri 2006) a partir de la propuesta: Lupiáñez, J.L. y Codina, A. (2002). Implementando problemas de optimización con calculadora gráfica. Trabajo presentado en el X Congreso sobre Enseñanza y Aprendizaje de las Matemáticas. El Ejido, Almería.a partir de una actividad de Jose Luis Lupiáñez Gómez y Antonio Codina Sánchez