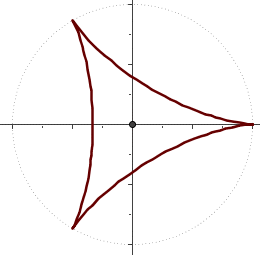
La Deltoide
-
Se
genera por un punto de una circunferencia que rueda en el interior
de otra de radio tres veces mayor:
-
También
se genera por un punto de una circunferencia que rueda en el interior
de otra cuyos radios están en relación 2/3:
-
Es la
envolvente de los diámetros
de un círculo 2a rodando en el interior de otro de radio 3a:
-
También
es la envolvente de las cuerdas de un círculo cuando los extremos
de la cuerda recorren la circunferencia en sentidos opuestos y uno
a velocidad el doble que el otro:
En
cuanto a la evoluta de una deltoide: ¿cuál es la curva envolvente
de la familia de rectas normales?
Experimentemos
con las podarias a una deltoide (la podaria de una curva respecto de un
punto fijo P es el lugar geométrico de los puntos de corte entre
cada tangente a la curva y su perpendicular por P):
¿Cómo
será la podaria a una deltoide respecto de su centro? ¿Y
respecto de un vértice? ¿Y...? Desliza el punto P y observa:
La antipodaria
de una curva respecto de un punto P es la envolvente de las perpendiculares
por cada punto Q de la curva a los correspondientes segmentos PQ. Comprueba
cuál es la antipodaria del trifolium respecto a su centro:
Si se lanzan
a una curva rayos paralelos entre sí, la envolvente de sus reflejos
en la curva es un tipo de caústica. Comprueba cómo son las
caústicas de la deltoide:
Si
quieres probar con rayos en otra dirección, pulsa el botón
 Actualizar antes
de mover el punto azul:
Creado con GeoGebra por Manuel
Sada Allo (Octubre 2006)
|
