LOGARITMOAK ETA FUNTZIO ESPONENTZIALA: ARIKETAK

1. Log2 = 0’301030 eta log3 = 0’477121 badira, kalkulatu:

a) log5 b) log24 c) log18 d) log(8/3)

2. log5 = 0’6989 bada, kalkulatu:

a) log50 b) log0’05 c) log500

3. Log2 = 0’301030 dela jakinik, kalkulatu:

a) b)

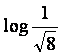
4. Aurkitu logaritmo hauen onarria:

a) log_a625 = 4 b) log_a0’0001 = 3 c) log_a0’01 = -2

5. Bata bestearen barruan sartzen diren Errusiako panpinak famatuak dira, panpina horien forma berdina da eta egurrezkoak dira, baina tamaina panpina bakoitzarena aurrekoarenaren 2/3 da. Kanpoko panpinaren egur kantitatea 360 cm³ da. Zenbat panpina badira txikienak 31’3 cm³ neurtzen badu?

6. Oilategi bateko populazioa hilabete batean, 1000 aletik 1300 aletara pasatzen da. Hazkunde esponentziala jarraitzen baldin badu, kalkulatu:

a) Populazioa eta denbora erlazionatzen duen funtzioa.

b) Urte bat barru, zein izango den populazioa.

c) Noiz izango diren 66541 ale.

7. Laku bat arrain mota berezi batekin birpopulatu dute. Gaur egun 136000 ale daude eta duela 3 urte 17000 arrain. Hazkundea esponentziala baldin bada, kalkula ezazu:

a) Arrain kopurua denboraren funtzioan adierazten duen funtzioa zein den.

b) Noiz izango dira 1000000 ale.

c) Duela zenbat urte sartu ziren lehenengo 132 aleak.

8. Oihana baten hazkundea ondoko funtzio honen bidez adierazten da,

F = A(1+i)^t , non F, t urte barru izango den egur kopurua den, A gaur egun dagoen egur kantitatea eta i urteko hazkundearen tasa den. Tasa hori mantentzen baldin bada, kalkula ezazue zenbat denbora behar den egurra kantitatea bikoizteko, i = 0’02 baldin bada.

9. C kapital bat banketxean ezartzen da %12 interespean. Zenbat urte pasako dira kapitala bikoizteko?

10. Progresio geometriko batean ondoko gaiak ezagutzen ditugu, 4, 8, 16, 32, …….131072. Zenbat gai daude? Logaritmoak erabili.

S oluzioak Atzera Aurrera