LOGARITMOAK ETA FUNTZIO ESPONENTZIALA:SOLUZIOAK

1) a) log5 = log(10/2) = 0’699 b) log24 = log(3.2³) = 1’3801

c) log18 = log(2.3²) = 1’2552 d) log(8/3) = log(2³/3) = 0’4259

2) a) log50 = log5 + log10 = 1’6989 b) log0’05 = log5 – log100 = -1’3010

c) log500 = log5 + log100 = 2’6989

3) a)

b)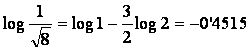

4) a) a = 5 ; 5⁴ = 625 delako. b) 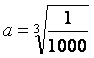; 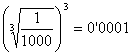delako.

c) a = 10; a^-2 = 0’01 delako.

5) 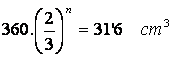beraz n = 6 panpina daude.

6) a) beraz formula da p = 1000.1’3^t. t hilabeteak izanik.

b) urte bat barru (12 hilabete) p = 1000.1’3¹² = 23298

c) 66541 = 1000.1’3^t orduan t = 16 hilabete barru.

7) a) orduan funtzioa hau da: p = 17000.2^t;

t urteak izanik.

b) 1000000=17000.2^t orduan t = 5’878 urte hau da 5 urte eta 10

hilabete eta erdi.

c) 136000=132.2^t orduan t = 10 urte pasa dira.

8) 2A = A.1’02^t orduan 2 = 1’02^t eta t = log2/log(1’02) = 35 urte.

9) 2C = C.1’12^t orduan 2 = 1’12^t beraz t = 6’116 urte hau da 6 urte eta hilabete bat.

10) a₁ = 4 eta r = 2 orduan 4.2^t-1 = 131072 orduan t-1 = 15 orduan t = 16 gai kopurua.

Atzera