BI
DIMENTSIOKO ESTATISTIKA DESKRIBATZAILEA: SOLUZIOAK
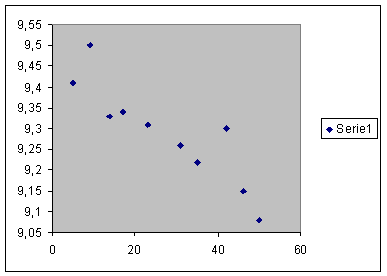
1) Puntu-hodeia
ondoko hau da:
x aldagaiaren
batezbestekoa 27,2 da; bere desbiderapena 15,12.
Y aldagaiaren batezbestekoa 9,29 da; bere desbiderapena 0,115.
Kobariantza -1,554 da eta r = - 0,89. Esan daiteke beraz,
korrelazioa sendoa dela eta negatiboa.
2) Eskatzen den
erregresio zuzena y = -0,00679x + 9,4747
da. 30 urteko txanpon bat hartuko
bagenu, bere pisua
-0,006.30+9,47 = 9,271 gramokoa izango
litzatekeela esan genezake.
3) Puntu-hodeia
ondoko hau da:
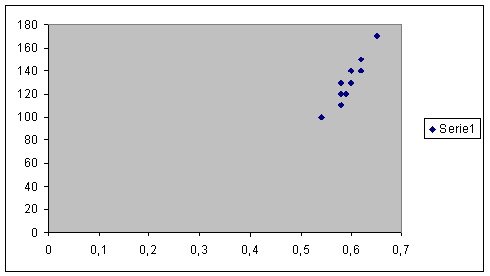
Ikusten da korrelazioa positiboa dela eta
sendoa ematen du. Korrelazio
koefizientea r = 0’945, beraz positiboa eta sendoa da.
4) x aldagaiaren batezbestekoa 11’6 da; bere
desbiderapenaren karratua 9’59.
Y aldagaiaren batezbestekoa
261 da. Kobariantza 127’9 da. Beraz y-ren erregresio zuzena x gainean ondoko
hau da:
Y = 13’33x + 106’29.
19 milioiko inbertsioa egiten badugu 13’33.19+106’29 = 359’56 salmenta
unitate espero dezakegu.
Korrelazio koefizientea r = 0’979
denez korrelazioa sendoa da eta estimatu dugun balioa daukagun taulatik ez
dagoenez oso
5) Grafikoa
ondoko hau da:
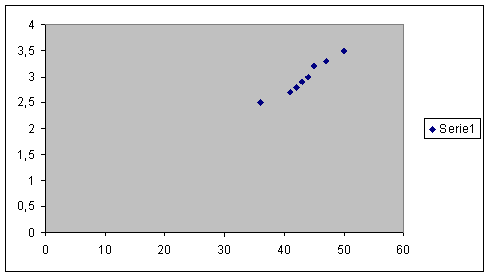
Bi aldagaien kobariantza 1’181 da.
Korrelazio koefizientea r = 0’975 da,
beraz bi aldagaien arteko erlazioa positiboa eta sendoa da.
6) a) Korrelazio
koefizientea r = 0’98 da.
b) Eboluzioa azter daiteke abiapuntutzat
harturik nekazaritzan jardun zuten estatuaren erregresio zuzena, lanean aritu
ziren
7) a) x aldagaiaren batezbestekoa 28’3 da; bere
bariantza 1206’44.
Y aldagaiaren batezbestekoa 51’5
da; bere bariantza 4807’25.
b) r = 0’0000119 beraz ez dago erlaziorik bien artean.
8) a) y – 7’25 =
9’33/86’3.(x – 46)
b) Estimatzen den kalifikazioa 8’1 da.