 5.2.-
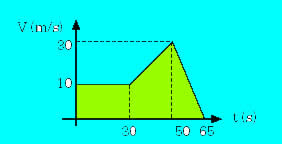
Dada la gráfica v-t de un vehículo de 600 kg de masa, determinar la fuerza que
actúa en cada tramo, así como el sentido de la misma.
5.2.-
Dada la gráfica v-t de un vehículo de 600 kg de masa, determinar la fuerza que
actúa en cada tramo, así como el sentido de la misma.Aplicar las leyes de Newton a la resolución de problemas de cuerpos sometidos a fuerzas que actúan en la misma dirección:
5.1.- Calcular la aceleración de un coche que soporta una fuerza motriz de 4500 N y una fuerza de rozamiento de 1300 N, sabiendo que su masa es de 860 kg..
Determinar la velocidad (en km/h) que alcanzará en 12 segundos, si parte del reposo y mantiene constante la aceleración.
 5.2.-
Dada la gráfica v-t de un vehículo de 600 kg de masa, determinar la fuerza que
actúa en cada tramo, así como el sentido de la misma.
5.2.-
Dada la gráfica v-t de un vehículo de 600 kg de masa, determinar la fuerza que
actúa en cada tramo, así como el sentido de la misma.
5.3.- Un microbús de masa 2500 kg que circula a 95 km/h frena bajo la acción de una fuerza de 3200 N. Hallar el espacio que recorrerá hasta que se pare y el tiempo que tardará.
*5.4.- Un cable tira verticalmente hacia arriba de un fardo de 250 kg. Determinar la tensión del cable en los casos siguientes:
a) El fardo asciende con aceleración de 2 m/s2 .
b) El fardo asciende con velocidad constante de 5 m/s.
c) El fardo está en reposo.
d) Desciende con velocidad constante de 12 m/s.
e) Desciende con aceleración de 2 m/s2 .
 *5.5.-
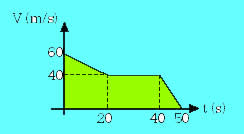
Un móvil de 50 kg lleva una velocidad que evoluciona con el tiempo de acuerdo
con la gráfica adjunta. Determinar la fuerza neta que soporta en cada uno de
los tramos del movimiento. Indicar también la dirección y sentido de la fuerza.
*5.5.-
Un móvil de 50 kg lleva una velocidad que evoluciona con el tiempo de acuerdo
con la gráfica adjunta. Determinar la fuerza neta que soporta en cada uno de
los tramos del movimiento. Indicar también la dirección y sentido de la fuerza.
5.6.- Un coche de 1200 kg de masa frena pasando de una velocidad de 108 km/h a otra de 36 km/h en un tiempo de 2 minutos. Determinar la aceleración , el espacio recorrido en los 2 minutos y la fuerza que soporta el automóvil.
 5.7.-
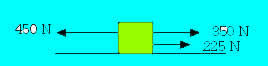
Sobre el bloque de la figura se ejercen las fuerzas que se indican en el gráfico.
El bloque se mueve soportando, además, una fuerza de rozamiento de 30 N. Dibujar
la fuerza de rozamiento y calcular la aceleración del bloque. La masa del bloque
es de 40 kg.
5.7.-
Sobre el bloque de la figura se ejercen las fuerzas que se indican en el gráfico.
El bloque se mueve soportando, además, una fuerza de rozamiento de 30 N. Dibujar
la fuerza de rozamiento y calcular la aceleración del bloque. La masa del bloque
es de 40 kg.
5.8.- Dos patinadores, de 50 kg y 60 kg de masa, respectivamente, se encuentran en reposo uno enfrente del otro. Si el primero aplica sobre el segundo una fuerza de 30 N durante un tiempo de 1,5 segundos, determinar:
a) La aceleración que adquiere el patinador de 60 kg mientras se le empuja.
b) La velocidad final con la que sale despedido.
c) ¿Qué le sucede al otro patinador?.
5.9.- Determina la aceleración de cada uno de los cuerpos de las figuras, aplicando la 2ª ley de Newton:

5.10.- Calcular la fuerza F para que los cuerpos de las dos figuras adquieran una aceleración de 0,5 m/s2 .

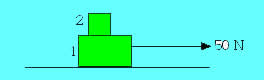
*5.11.- Hallar la masa del cuerpo 2 si la masa del cuerpo 1 es de 30 kg y el sistema adquiere una aceleración de 1,5 m/s2 cuando se ejerce una fuerza de 50 N.
5.12.- Sobre un cuerpo de 7 kg de masa que descansa en una superficie horizontal se aplica una fuerza de 35 N en la dirección del plano. Hallar la fuerza de rozamiento, si:
a) El cuerpo adquiere una aceleración de 2 m/s2
b) El cuerpo se mueve con velocidad constante de 5 m/s.
5.13.- Calcular la masa de un cuerpo que , bajo la acción de una fuerza de 12 N, cambia su velocidad de 3 m/s a 11 m/s en un tiempo de 4 segundos.
*5.14.- Calcular la fuerza de rozamiento que soporta un coche que se mueve en un plano horizontal con velocidad inicial de 23 m/s si recorre 150 m antes de parar. La masa del coche es de 1200 kg.. ¿Qué hubiera sucedido si la masa del coche fuese de 600 kg , siendo la misma la fuerza de rozamiento?.
5.15.- El cuerpo de la figura pasa de una velocidad de 12 m/s a otra de 18 m/s en un tiempo de 8 segundos. Hallar la fuerza de rozamiento.
