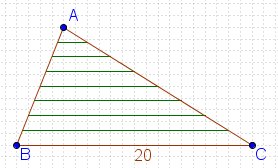
3. SEGMENTOS EN UN TRIÁNGULO En el triángulo ABC, dibujamos siete segmentos paralelos al lado BC, que dividen en 8 partes iguales al lado AC. Si BC = 20 centímetros, ¿cuál es la suma de las longitudes de los 7 segmentos? (Tomado de los Retos Matemáticos propuestos por Santiago Fernández en Divulgamat)

1. Utiliza los botones de navegación, en la ventana de debajo, para observar una posibilidad de construcción con GeoGebra. Mueve los vértices del triángulo y observa los cambios en las medidas.
2. Luego intenta reproducir la construcciónen la ventana de la derecha, utilizando las herramientas disponibles.

3. Pero claro, el método anterior nos ha servido gracias a que, tratándose de 7 segmentos (que dividen los lados en 8 partes iguales), los puntos medios nos facilitan la construcción. ¿Hubiese sido tan sencillo con, por ejemplo, 13 en lugar de 7 segmentos?

Busca alguna regularidad en la figura para idear un método alternativo.

Creado con GeoGebra por Manuel Sada Allo (Agosto 2009)