
1. PATIOA
Eskola bateko patioan horma bat eta zuhaitz bi daude. Umeak ondoko jolasa egiten dabiltza: zuhaitz batetik bestera doaz tartean horma ikutu behar dutelarik. Ibilbide irabazlea zein den badakizu?
[PUIG ADAM, P. - REY PASTOR, J. Elementos de Geometria. 82. horrialdea]
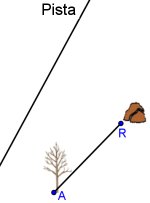
2. ALTXORRA
Basamortu batean, oso nekatuta eta hilzorian dagoen abenturazale ospetsu batek altxor bat gorde du. A (zuhaitz lehorra kokatuta dagoen puntua), R (haitza kokatuta dagoen puntua), P (pista edo bidearen puntu ezezagun bat) eta T (altxorra gordeta dagoen puntua) erronbo baten lau erpinak direla besterik ez dakigu. Altxorra aurkitzeko, non egin beharko genuke zuloa? Zenbat aukera desberdin daude?
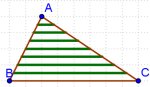
3. ZUZENKIAK TRIANGELU BATEAN
ABC triangeluan, BC zuzenkiarekiko paraleloak diren zazpi zuzenki irudikatu ditugu; zazpi zuzenki hauek AC aldea 8 zatitan banatzen dute. BC = 20 zentimetrotakoa bada, zein da 7 zuzenkien luzeren batura?
(Santiago Férnandezek Divulgamat-en proposatutakoa; Retos Matemáticos-etik hartua)

4. ARROSA-LEIHOA
4 lobuludun arrosa-leiho bat eraiki ezazu. Zein da barne zirkunferentzien erradioen eta kanpo zirkunferentziaren erradioaren arteko erlazioa?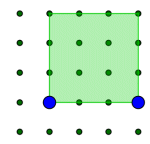
5. KARRATUAK GEOPLANOAN
Zenbat karratu desberdin eraiki daitezke 4x4-ko geoplano batean?
6. FUTBOLARI BATEN JAURTIKETA ANGELUA
Zein posizio desberdinetatik lor daiteke, futbolari baten atearekiko jaurtiketa angelua, penalti puntutik lortzen denaren berdina izatea?

7. POTENOT-EN PROBLEMA
Itsasontzi batetik kostaldeko A, B eta C puntu nabariak ikusten dira. Begi-lerroek osatzen dituzten AXB eta BXC angeluak neurtzen dira. Datu erraz bi hauekin, mapan itsasontziaren X posizioa zehaz daiteke.
( P. Puig Adam-en "Elementos de Geometría métrica", 86. orrialdea)

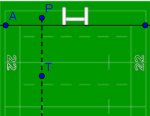
8. RUGBY PROBLEMA
Rugby jokalari batek entsegu bati jarraitzen dion tranformazio saioan, zein puntu aukeratu behar du, atea ikusteko angelua maximoa izan dadin?
Azalpena: Jokalari batek, (AB) entsegu lerroa baino haragoko (P) puntuan baloia uztea lortzen duenean, P-tik igaro eta AB-rekiko perpendikularrean berak aukeratutako (T) puntu batetik jaurtiketa egiteko eskubidea du.

9. HORIZONTEA
Itsasoari begira... zein distantziatara dago horizontea?
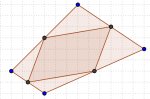
10. ERDIKO PUNTUAK
Kalkula ezazu poligono baten, eta bere aldeen erdiko puntuak lotzean lortutako poligonoaren arteko arrazoia
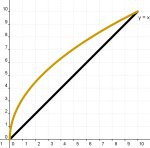
11. NOTEN BIRDOIKETA
Bigarren hezkuntzako eskola bateko ikasle bat etxera joan da, matematikako irakaslea ikasleek funtzioei buruzko froga idatzi batean lortutako emaitzekin gustora geratu ez dela esanez. Irakaslea, azterketako galderak zailegiak izan direla ikusita, nota hauek zuzenketa faktore bat erabiliz "egokitzea" erabaki du.
Zein zuzenketa faktore proposa diezaizkiogu irakasleari notak aldatzeko? Era algebraikoan eta grafikoki adieraz itzazu. Bakoitzaren abantailak eta desabantailak azter itzazu.
( http://www.socylema.es/congresosegovia/ponencias/Modelizacion%20Matematica.doc-en Abraham Arcavi eta Constantino de la Fuenteri hartua )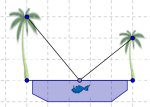
12. BI PALMONDO
Errekaren bi ertzetan, palmondo bi hazi dira bata bestearen parean . Hauetako baten altuera 30 ukondotakoa da eta bestearena 20koa. Enborren arteko distantzia 50 ukondotakoa da. Palmondo bakoitzaren adaburuan, txori bat dago. Bapatean txori biek palmondoen artean, uretan, arrain bat ikusi dute.
Txori biak arrainaren bila joan eta bertara une berean ailegatu dira. Palmondo handiaren enborretik zein distantziatara egon da arraina? (Txori biak abiadura berean joan direla suposatu behar dugu).
(XI. mendeko matematikari arabiar baten lanean agertzen da)