Ejemplos de Problemas para ser explorados / construídos / trabajados / resueltos con el apoyo de GeoGebra |
Pulsando el botón de debajo puedes intentar dibujar o crear construcciones, con GeoGebra, para la exploración y resolución de los problemas propuestos.
Si no encuentras la solución puedes utilizar los enlaces que te ayudarán a ver posibles caminos.
 |
1. EL PATIO En el patio de una escuela hay una pared y dos árboles. Los niños realizan el siguiente juego: van de un árbol a otro pero por el medio deben tocar la pared. ¿Sabrías encontrar la trayectoria ganadora? [PUIG ADAM, P. - REY PASTOR, J. Elementos de Geometria. pàg 82] |
||||
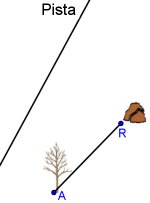 |
2. EL TESORO En un desierto, un legendario aventurero, agotado y al borde de la muerte, ha enterrado un tesoro. Sólo se sabe que los puntos A (donde el árbol seco), R (donde la roca), P (un punto desconocido de la pista) y T (donde está enterrado el tesoro) son los cuatro vértices de un rombo . ¿Dónde habría que cavar para buscar el tesoro? ¿Cuántas posibilidades diferentes hay?
|
||||
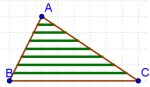 |
3. SEGMENTOS EN UN TRIÁNGULO En el triángulo ABC, dibujamos siete segmentos paralelos al lado BC, que dividen en 8 partes iguales al lado AC. Si BC = 20 centímetros, ¿cuál es la suma de las longitudes de los 7 segmentos? (Tomado de los Retos Matemáticos propuestos por Santiago Fernández en Divulgamat) |
||||
 |
4. EL ROSETÓN Construir un rosetón de 4 lóbulos exacto. ¿Qué relación hay entre los radios de las circunferencias interiores y el de la circunferencia exterior? |
||||
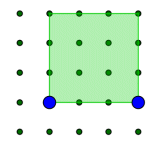 |
5. CUADRADOS EN EL GEOPLANO ¿Cuántos cuadrados diferentes se pueden construir en un geoplano 4x4? |
||||
 |
6. EL ÁNGULO DE TIRO DE UN FUTBOLISTA ¿Desde qué diferentes posiciones el ángulo de tiro de un futbolista respecto a la portería es el mismo que desde el punto de penalti? |
||||
 |
7. EL PROBLEMA DE POTENOT Desde un navío se observan tres puntos notables de la costa A, B y C, y se miden los ángulos AXB y BXC que forman entre sí las visuales. Con estos dos sencillos datos se puede fijar en el mapa la situación X del navío. (pág.86 de "Elementos de Geometría métrica" de P. Puig Adam) |
||||
|
|
8. EL PROBLEMA DEL RUGBY ¿Qué punto debe elegir un jugador de rugby, en el intento de transformación que sigue a un ensayo, para que el ángulo con el que se ve la portería sea máximo? Aclaración: Cuando un jugador consigue depositar el balón en un punto (P) tras la línea de ensayo (AB), tiene derecho a lanzar desde un punto (T), elegido por él, en la prependicular a AB por P
|
||||
 |
9. EL HORIZONTE Mirando al mar... ¿A qué distancia está el horizonte? |
||||
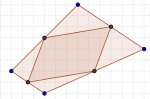 |
10. PUNTOS MEDIOS Determinar la razón entre el área de un polígono y la del obtenido al unir los puntos medios de sus lados |
||||
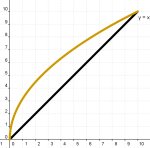 |
11. EL REAJUSTE DE LAS NOTAS Un estudiante de escuela secundaria regresó a su hogar contando que su profesora de matemáticas estaba descontenta con las calificaciones de sus alumnos en una prueba escrita que habían realizado sobre funciones, atribuyéndolo a que quizá las preguntas propuestas habían sido un tanto difíciles. La profesora decidió “ajustar” esas calificaciones usando un factor de corrección. ¿Qué factores de corrección podemos proponer a la profesora para que modifique las notas? Expresarlos en forma algebraica y representarlos gráficamente. Analizar las ventajas e inconvenientes de cada uno. (Tomado de Abraham Arcavi y Constantino de la Fuente en http://www.socylema.es/congresosegovia/ponencias/Modelizacion%20Matematica.doc ) |
||||
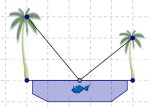 |
12. DOS PALMERAS A ambas orillas del río crecen dos palmeras una frente a la otra.
La altura de una es de 30 codos y la de la otra de 20. La distancia entre
los troncos es de 50 codos. En la copa de cada palmera hay un pájaro.
De súbito los dos pájaros descubren un pez que aparece en
la superfcie del agua, entre las dos palmeras. |
||||